| Автор | Сообщение |
|
Ять
|
| постоянный участник


|
Пост N: 121
Зарегистрирован: 27.08.07
|
|

Отправлено: 04.11.09 08:11. Заголовок: Деды и Бабы (прод. 9)
Молчат гробницы, мумии и кости, — Лишь слову жизнь дана Из древней тьмы, на мировом погосте, Звучат лишь Письмена И нет у нас иного достоянья' Умейте же беречь Хоть в меру сил, в дни злобы и страданья, Наш дар бессмертный — речь И Бунин «Слово» https://yandex.ru/video/touch/preview/?text=%D0%B7%D0%B0%D1%87%D0%B5%D0%BC%20%D0%B8%20%D0%BE%20%D1%87%D0%B5%D0%BC%20%D0%B3%D0%BE%D0%B2%D0%BE%D1%80%D0%B8%D1%82%D1%8C.%20%D1%80%D0%BE%D0%BC%D0%B0%D0%BD%D1%81.%20%D0%B8%D0%B2%D0%B0%D0%BD%20%D0%B1%D1%83%D0%BD%D0%B8%D0%BD%20%D1%81%D1%83%D1%85%D0%B0%D0%BD%D0%BE%D0%B2%20%D0%B0&path=wizard&parent-reqid=1634894748464244-960788254299574674-sas3-0893-4f3-sas-l7-balancer-8080-BAL-7176&wiz_type=vital&filmId=9215601213055833008 Зачем и о чём говорить? Стихотворение Иван Бунин написал в 1890 г. (опубл.: Орловский вестник. 1891. № 22, 22 янв.). Оно перекликается со знаменитым тютчевским Silentium! ("Молчи, скрывайся и таи") …Зачем и о чём говорить? Всю душу, с любовью, с мечтами, Всё сердце стараться раскрыть — И чем же? — одними словами! И хоть бы в словах-то людских Не так уж всё было избито! Значенья не сыщете в них, Значение их позабыто! Да и кому рассказать? При искреннем даже желанье Никто не сумеет понять Всю силу чужого страданья!  ШТО НА НЯ ДИВИШ??? НИГДА РУСИНА НЕ ВІДІВ??? В лето 6983<...> Того же году обретох написание Офонаса тверитина купца, что былъ в Ындее 4 годы[с середины 1471 до начала 1474] ...А в том в Чюнере ханъ у меня взял жеребца, а увядал, что яз не бесерменянин - русинъ Хождение за три моря Афанасия Никитина. https://web.archive.org/web/20101228023336/http://kirsoft.com.ru/freedom/KSNews_452.htm |  |

|
|
Ответов - 300
, стр:
1
2
3
4
5
6
7
8
9
10
All
[только новые]
|
|
|
Ять
|

| постоянный участник


|
Пост N: 5163
Зарегистрирован: 27.08.07
|
|

Отправлено: 05.03.23 12:54. Заголовок: Жовто-блакитная Хаза..
Жовто-блакитная Хазария  Cиониcты взяли власть в России и в бывших советских республиках и сталкивают нас между собой. Свой каганат у нас они строят с такой же жестокостью, с какой уничтожают палестинцев на их земле. Только здесь они расчищают территорию нашими руками. Вполне возможно, сливать Новороссию как территорию не будут. Ее будут использовать для взаимного уничтожения русских и украинцев, все более углубляя раскол, который со временем перейдет в открытое военное противостояние Украины и России. А пока здесь выгодна вялотекущая война с переменным успехом. Если для пиара российского руководства нужно будет взять Славянск или Мариуполь, ополчению разрешат их взять. Власть в Киеве и Москве в одних и тех же руках, и кто кому какой кусок земли перепихнет – для них не имеет значения. Все, что исходит от Москвы, лукаво. Лукавы заявления о помощи. Лукавство – гумконвои, которые не доходят до людей и распродаются на рынках. Лукавы речи о Русском мире и противостоянии Западу. Лукавы войны, которые они ведут. Лукав мир, который они якобы хотят установить. Все ложь, измена и обман. Лукавое не имеет веса и цены. Но дорого платит тот, кто поверил. "РАЗДЕЛЯЙ и ВЛАСТВУЙ" - вот та схема, с которой враг пришёл на нашу славянскую землю. И он добился своего. Враг разделил славянский народ на части и посеял хаос и войну. Славяне убивают славян на радость врагам! В этой славянской бойне победителей не будет, все славяне окажутся в проигрыше...В выигрыше окажутся лишь те, кто все эти "перестроечные" годы вёл политику РАЗДЕЛЕНИЯ и НАТРАВЛИВАНИЯ. По сценарию, который отрабатывают российские СМИ, русский народ борется с «украинским фашизмом». По сценарию украинских СМИ «украинцы защищают единство своего государства». Какие удачные грабли! Как в Гражданскую войну. Опять у русских идеи разные, а у их исконных врагов одна – стравить простофиль и грабить, пока те будут рвать чубы друг другу за «правое дело». Они - как бы всегда порознь, но на деле вместе и их цели одни и те же всегда — создание единой иyдейcкой общины в славянских странах. Мы же всегда как бы вместе и неразлучны, но на деле оказываемся смотрящими друг на друга в оптические прицелы. Наша конечная цель это просвещение и осознание того, что все технологии и СМИ направлены лишь на разъединение славянского единства выгодное лишь пришельцам и инородным паразитам... " - Алексей Мозговой, 2014 по май 2015 гг. От Игоря Ивановича Стрелкова: Персонально для ув. Андрея Морозова ("Мурза") сообщаю: если-бы уважаемый Андрей не истерил на ровном месте, не обвинял (совершенно безосновательно) других во вбрасывании ложных версий от ФСБ" и не настаивал на себе, как на единственном источнике достоверной информации и абсолютном координаторе "неформального расследования", то сегодня ему-бы, возможно, не пришлось констатировать, что с момента убийства Игоря Мангушева ("Берега") прошло 30 суток, а уголовное дело до сих пор не заведено и, с высокой вероятностью, заведено уже не будет (как до сих пор не расследованы убийства Мозгового и Беднова, совершенные "вагнеровцами" в 2014-м году по приказам Суркова-Плотницкого). "23 февраля 2014 г. началась Русская революция на Украине.... 📌🔥 24 и 25 восстание против хунты и за Россию перекинулось на все города Крыма. После этого восстание началось в Донецке, Луганске, Мариуполе, Херсоне, Запорожье, Харькове, Одессе, Николаеве, Днепропетровске. 💥Несколько дней Кремль думал. Наконец 26 февраля военные оказали помощь крымчанам. Только крымчанам. К сожалению. 💥Поэтому карательные фашистские отряды созданные хунтой и олигархами типа Коломойского, подавили восстание в Харькове, Одессе, Николаеве, Херсоне, Днепре. 📌🔥 Это была самая большая ошибка - не ввести армию России на Украину весной 2014 года. Россия сейчас расплачивается за ту ошибку весны 2014 года." Сергей Марков, ТГ-канал "Логика Маркова" 🔔 Учитывая 8 лет последующего бездействия, ликвидации всех русских полевых командиров, лицемерного сочувствия "самопровозглашенным" народным республикам и год странной во всех отношениях СВО - может так предателями во власти и было задумано? 🔔 |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5165
Зарегистрирован: 27.08.07
|
|

Отправлено: 06.03.23 17:38. Заголовок: К бозе Дхи ПРЕОБРАЗО..
К бозе Дхи ПРЕОБРАЗОВАНИЕ БОГОЛЮБОВА И ПЛАНИМЕТРИЯ ЛОБАЧЕВСКОГО  загрузить картинку в интернет загрузить картинку в интернет Н.А. Черников. ОИЯИ, Дубна Установлена связь преобразования Боголюбова в теории сверхтекучести с планиметрией Лобачевского в двух конформно-евклидовых моделях Пуанкаре. 21 Октября 1946г. на сессии Физико-математических наук отделения Академии наук Союза Советских Социалистических Республик Н.Н. Боголюбовм (1909-1992) выступил с докладом о развитой им квантовой микроскопической теории сверхтекучести [1, c.215]. К гамильтониану сверхтекучей системы Боголюбов применил замечательное преобразование бозе-операторов, называемое преобразованием Боголюбова https://vk.com/s/v1/doc/kZCiUDi6iw6TgHVCdF_hgMNWT5OAdAaLFg1ieVfQ2bSNQuXmOeM НИКОЛАЙ АЛЕКСАНДРОВИЧ ЧЕРНИКОВ http://theor.jinr.ru/people/Chernikov/works.html https://www.mathnet.ru/php/person.phtml?option_lang=rus&personid=20809 Сто лет СТО https://vk.com/s/v1/doc/i47YLQVsDaDLlyMWpij-WIJPL7DsWonkW6Wce6PvSC-32wppggg СПИСОК ЛИТЕРАТУРЫ 1. Боголюбов Н.Н. К теории сверхтекучести// Избранные труды в трех томах. Киев, 1970. Т.2. С.210-224; Изв. АН СССР. Сер.физ. 1947. Т.11, №1. С.77-90. 2. Боголюбов Н.Н. Вопросы теории сверхтекучести бозе- и ферми-систем // Избранные труды в трех томах. Киев, 1971. Т.3. С.11-16; Вести.АН СССР. 1958. Т. 28, вып. 4. С.25-29. 3. Черников Н.А. К истории открытия Лобачевским неевклидовой геометрии // Письма в ЭЧАЯ. 2002.№ 3[112]. C. 5-18. 4. Черников Н.А. Ведение геометрии Лобачевского в теорию гравитации // ЭЧАЯ. 1992. Т.23, вып.5. С.1155-1191. 5. Лобачевский Н.И. О началах геометрии //Казанский вестник. Т.4. Вып. ХХV. Кн.II-III. Февраль-март 1829 г. С. 178-187; Кн.IV.Апрель 1829 г. С.228-241; Вып. XXVII. Кн. XI-XII. Ноябрь-декабрь 1829 г. С.227-243; Вып. XXVIII. Кн. III-IV. Март-апрель 1830 г.С.251-283; Вып. XIX. Кн. VII-VIII. Июль-август 1830 г. С.571-636. 6. Лобачевский Н.И. Полн. собр. соч.М.; Л., 1946. Т.1. С. 185-261. 7. Привалов И.И. Введение в теорию функций комплексного переменного. М.; Л.: ОГИЗ; Гостехиздат, 1948. 452 с. 8. Бушманова Г.В., Норден А.П. Элементы конформной геометрии. Казань: Изд-во Казанск. ун-та, 1972. 178 с. 9. Пуанкаре А. Теория фуксовых групп // Об основаниях геометрии: Сб. классических работ по геометрии Лобачевского и развитию ее идей. М., 1956. С.304-306. 10. Черников Н.А. Планиметрия Лобачевского, модель Пуанкаре и преобразование Боголюбова в теории сверхтекучести. Препринт ОИЯИ Р2-94-469. Дубна, 1994; Междунар. Боголюбовский сим. "Фундаментальные проблемы теоретической и математической физики", Дубна, 18-21 августа 1994 г. |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5166
Зарегистрирован: 27.08.07
|
|

Отправлено: 08.03.23 11:02. Заголовок: Москва, 7 марта - Аи..
Москва, 7 марта - АиФ-Москва.  За Международный женский день стоит сказать спасибо активисткам Кларе Цеткин и Розе Люксембург, по инициативе которых учрежден этот праздник, заявил министр обороны РФ Сергей Шойгу, выступая в Центральном академическом театре Российской армии. «Благодаря им у нас появился еще один день, в который мы можем сказать слова благодарности, любви, обожания нашим дорогим женщинам», - сказал он перед церемонией чествования женщин-военнослужащих. Шойгу отметил, что в этот день вспоминают бабушек, мам, дочерей, сестер. «Кто-то и так часто вспоминал. Кто-то забыть не может. Кстати, тещ тоже вспоминаем», - пошутил министр. https://aif.ru/society/army/shoygu_poblagodaril_klaru_cetkin_i_rozu_lyuksemburg_za_8_marta Когда отмечается Пурим в 2023 году Как и многие еврейские красные дни календаря, долгожданный для всех иудеев Пурим берет свое начало из другой памятной для иудеев даты — поста Эстер, или, правильнее сказать, поста Эсфири. Пурим относится к категории религиозных еврейских торжеств. Ими чрезвычайно богата история иудеев. Постятся евреи в двенадцатом месяце своего календаря. Его имя — адар, и длится этот отрезок времени с 20 февраля по 24 марта. Непосредственно сам Пурим, как и все еврейские праздники, начинается в сумерках одного дня и заканчивается через день, когда солнце также начинает клониться к закату. В Израиле дату празднования Пурима определяют по лунному календарю. Если брать более привычное григорианское летоисчисление, то дата всеобщего еврейского веселья наступает в середине первого весеннего месяца. Таким образом, Пурим 2023 должен начаться вечером 6 марта и завершиться вечером 7 марта. История праздника Пурим Окунемся в глубокую древность, когда в 586 году до нашей эры правитель Вавилона Навуходоносор разрушил Иерусалим и обрек евреев на полувековое рабство. Еврейское рабство продолжалось, и когда власть в Вавилонском царстве перешла к персам. Персидский царь Ксеркс Первый решил взять в жены девушку Эсфирь, не подозревая о ее еврейском происхождении. Это все сопровождалось полугодичными торжествами в честь превосходства над иудеями. Смелая Эсфирь, выйдя замуж за персидского правителя, стойко противостояла попыткам окружения своего супруга уничтожить еврейский народ. Жребий (пур) уничтожения выпал на тринадцатое адара. Параллельно против Ксеркса плелся заговор, однако Эсфирь сумела предотвратить покушение на мужа. Как в сказках со счастливым концом, все в итоге раскрылось. Трехсуточные молитвы Эсфири возымели действие. Ксеркс Первый поверил жене. Не в силах отменить свой указ об уничтожении евреев, он позволил им защищаться. При нападении персов тринадцатого числа евреи стойко оборонялись и одержали победу. На следующий день началось празднование освобождения еврейского народа из персидского плена, получившего название Пурим (от множественного числа). Естественно, современные израильтяне и евреи всего мира, чтящие свою богатую древнюю историю, празднуют чудесное спасение нации. Делают они это шумно и ярко. https://www.kp.ru/family/prazdniki/purim/ Праздник этот придуман в 1910 году еврейской большевичкой Розой Люксембург и феминисткой Кларой Цеткин. Придумали этот праздник, который был утвержден в следующем, 1911 году, на Европейской конференции женщин-социалисток. День 8 марта подозрительно “удачно” пришелся на празднование иудейского праздника Пурим. Пурим празднуется в честь “подвига” Есфири... https://proza.ru/2017/01/04/1006 |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5168
Зарегистрирован: 27.08.07
|
|

Отправлено: 08.03.23 18:47. Заголовок: Несущая свет https:/..
Несущая свет  Традиции понимания материнства в русской культуре воспроизводились первоначально через призму языческой культуры. Основной функцией материнства в данный период являлась трансляция ценностей и обрядов. Материнство занимало пограничное положение между природой и культурой, а женщина заключала в себе исторически сформированный образ матери. Несмотря на то, что славянские племена территориально были разрозненны, многие из культов были сходны. В них женщина-мать сравнивалась с образом Матери-Земли, а Богиня-Матерь считалась воплощением воспроизводящей силы природы, «оплодотворенная» дождем она давала урожай, кормила людей, помогала продолжить род [9]. Значительную роль в жизни славянских племен играло также поклонение богине, олицетворяющей Женскую Любовь. Богиня Лада являлась покровительницей матерей и детей, «помогала» в родах. То, что люди приписывали к основным функциям Лады (созидание и покровительство семье), становилось основанием женской ментальности. Женское, материнское начало образовало архаичный пласт культуры, через который можно проследить культурные феномены от индивидуальных до родовых [10, с. 86–88]. Таким образом, в языческой культуре образ Матери-Земли придавал женщине черты плодородности, мудрости, родственной близости, лишенной эротичности. Священность женщин находилась в прямой зависимости от святости Земли, а способность женщины к рождению детей имела космическую модель, стоящую на высокой ступени духовности. Впоследствии с принятием христианской религии культ Богини-Матери был заменен образом Богородицы, носящим сходные черты. А трансформация языческой мифологии привела к созданию материнского архетипа, в котором женщине были приписаны жертвенность, скромность, сострадание, любовь, асексуальность, целомудрие. В работах русских философов материнство определялось как особенная черта женской природы. Н. А. Бердяев, ставивший в основу мировоззрения проблему человека, рассматривал материнство как «космическое начало заботы и охраны жизни от грозящих ее опасностей» [11, с. 55]. Философский взгляд Г. П. Федотова заключался в понимании божественного материнства как сердца русской религиозности. Главной особенностью исследования темы материнства в русской философской мысли было присутствие культа Софии – «Божественной мудрости». Данное понятие рассматривалось в работах С. Н. Булгакова, где он ставил концепт Софии в идеальную основу мироздания, воспринимая ее как предмет божественной любви и вечной Женственности. В своем произведении «Свет невечерний» он рассматривал процесс рождения ребенка для женщины, главным образом, не как болезненный и опасный, а как дающий жизнь новому человеку. При этом Булгаков указывал на радость, с которой мать и отец встречают появившегося ребенка, подчеркивал ощущение родителями того, что только появившийся человек существовал с ними всегда [12, с. 400–415]. Философский взгляд В. В. Розанова на семейные отношения основывался на религиозном восприятии мира. В своих трудах он указывал, что общий упадок культуры отражается и в семье, в первую очередь в отказе от деторождения. В работе «В мире неясного и нерешенного» Розанов рассматривал четыре фазы творения: чадо-зачатие, чадо-вынашивание, чадо-рождение, чадо-воспитание. В первой фазе проявлялось творение мира – «главный трансцендентно-мистический акт». В чадо-вынашивании и чадо-рождении человек раскрывался как сосуд Божьей Тайны. Чадо-воспитание возлагалось на родителей и являлось рациональной категорией. Розанов восхищался женщиной, ставил ее ключевой фигурой, указывал на божественное равенство полов [13, с. 122–123]. Качественно иные взгляды на рассматриваемую проблематику были заложены в марксизме. Основные представители – Ф. Энгельс в работе «Происхождение семьи, частной собственности и государства» [14], А. Бабель в произведении «Женщина и социализм» [15], К. Цеткин в трудах «Женский вопрос», «Международный женский коммунистический день» [16; 17] – разрабатывали идею равенства полов, признания материнства одной из главных социальных функций, совмещения материнства с другими видами деятельности. В данных произведениях авторы подчеркивали ценность охраны женского труда и своеобразной поддержки материнства... 9. Токарев С. А. Ранние формы религии и их развитие / С. А. Токарев. – Изд. 2-е. – М., 2011. – 400 с. 10. Кабакова Г. И. Дети некрещеные / Г. И. Кабакова // Славянские древности : этнолингвистический словарь : в 5 т. / под общ. ред. Н. И. Толстого. – М., 1999. – Т. 2. – С. 86–88. 11. Бердяев Н. О назначении человека / Н. Бердяев. – М. : Республика, 1993. – 383 с. 12. Булгаков С. Н. Свет невечерний : созерцания и умозрения / С. Н. Булгаков. – М. : Республика, 1994. – 415 с. 13. Розанов В. В. В мире неясного и нерешенного / В. В. Розанов. – М. : Республика, 1995. – 462 с. 14. Энгельс Ф. Происхождение семьи, частной собственности и государства : избранные произведения : в 3 т. / Ф. Энгельс. – М. : Политиздат, 1986. – Т. 3. – 639 с. 15. Бабель А. Женщина и социализм / А. Бабель. – М. : Госполитиздат, 1959. – 596 с. 16. Цеткин К. Женский вопрос : пер. с нем. / К. Цеткин. – Гомель : Гомельский рабочий, 1925. – 70 с. 17. Цеткин К. Международный женский коммунистический день : доклад на собрании агитаторов в МК РКП (б) 12 февраля 1925 года / К. Цеткин. – М. : Моск. рабочий, 1925. – 61 с. Белогурова Ю.Г. Представление о материнстве в западноевропейской и русской философской мысли // Вестник Воронежского государственного университета. Серия «Философия». 2014. № 1 (11). с.45-51 http://www.vestnik.vsu.ru/search_ru.asp |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5171
Зарегистрирован: 27.08.07
|
|

Отправлено: 09.03.23 15:02. Заголовок: Принцип относительно..
Принцип относительности и Геометрия Лобачевского Проективное пространство скоростей 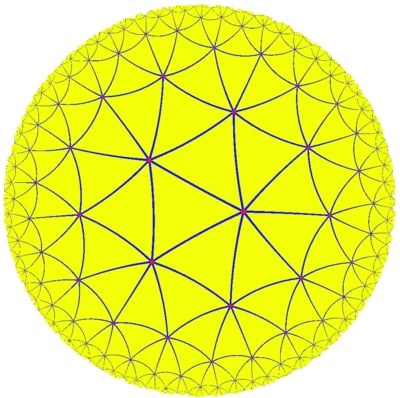 Се ТрГлаве молiхомь Влiце а Мале Замощение плоскости Лобачевского правильными треугольниками ({3;7}) ...Первые шаги в формировании соответствующего взгляда на механику был предпринят еще самим Лобачевским [31], а также (несколько более конкретной форме) Де-Тилли [81], [82], Дженокки [85] и Шерингом [108], [109], в связи с выяснением возможности построения механики пространств Лобачевского. Опираясь на известную аналогию между кинематикой и статикой твердого тела в евклидовом пространстве и пытаясь перенести ее в механику неевклидова пространства, они столкнулись с необходимостью построения новой теории векторов, пригодной для неевклидовых пространств. Дальнейшее развитие этого круга идей с привлечением аппарата проективной геометрии был осуществлен в работах Линдемана [96], Клиффорда [79], Кокса [80] и Бухгейма [77]. Помимо обычных векторов (пар точек) они рассматривали как элемент теории векторов пары плоскостей и пары прямых. В соответствии с этим в векторную алгебру были введены комплексные числа с двумя единицами. До логического завершения эта теория была доведена А.П. Котельниковым [28]. И был открыт так называемый принцип соответствия, позволяющий свести изучение сложных объектов этой теории к изучению гораздо более простой модели — связки векторов в евклидовом пространстве. Открытие Эйнштейном специальной теории относительности придал этим исследованиям новое направление — выяснением связи геометрии пространства скоростей в специальной теории относительности и пространстве Лобачевского. По-видимому, впервые на эту связь обратил внимание в 1909 году Зоммерфельд [111], а затем, независимо, Варичак [120], Герглоц [88] Роб [107]. Далее, в 1914 год появился русский перевод статьи Клейна [27], стимулировавшей работы Казанской школы геометров. Клейн доказал, что группа Лоренца изоморфна группе движений пространства Лобачевского. В 1923 год A.П. Котельниковым [30] связь между геометрией Лобачевского и специальной теорией относительности была установлена полностью. А.П. Котельников, представляя скорости частиц в виде бесконечно удаленной точки пространства-времени, ввел проективное пространство скоростей. В этом пространстве скорость частиц с нулевой массой покоя (фотона) лежит на абсолюте, скорость частиц с положительной массой покоя — внутри абсолюта, а скорость частиц с мнимой массой покоя (такие частицы сейчас называют тахионами)—вне абсолюта. При этом внутренняя область абсолюта представляет собой пространство Лобачевского с характерной константой с, равной скорости света. Интерес к этим исследованиям вновь возродился лишь в середине пятидесятых годов, в связи с появлением в свет книги В.A. Фока [57] и работы Н.А. Черникова [58]. В упомянутой книге В.A. Фока введение пространства скоростей Лобачевского основано на формулах Эйнштейна-Пуанкаре для относительной скорости частиц и модели Бельтрами геометрии Лобачевского. В отличии от В.A. Фока, построение Н.A. Черникова основано на введение расслоенного пространства. Поясним основную идею построения Н.А. Черникова. Пространство-время теории относительности представляет собой гладкое многообразие, в котором траекториям частиц соответствуют гладкие кривые. Касательные к этим кривым представляют собой скорости частиц. Таким образом, в каждой точкe x из М^4 пространство скоростей частиц представляет собой проективно трехмерное пространство. Пространство же всех скоростей частиц представляет собой семимерное пространство с базой М^4 и слоем Р^3(x). При этом дифференциалы координат многообразия М^4 представляют собой однородные координаты в Р^3(x). Зададим в слое Р^3(x) метрику gijdxdx с сигнатурой (+ , - , - , -) . Для обычных частиц gijdxdx>0. Эта область представляет собой пространство Лобачевского с характерной константой с, равной скорости света. Скорости частиц с нулевой массой покоя (фотонов) определяются условием gijdxdx = 0, а частиц с мнимой массой (тахионов) — условием gijdxdx<0. Более детальное развитие теории пространства скоростей можно найти в работах Н.А. Черникова [58] — [68]. В настоящее время этот подход уже систематически используется рядом физиков (см.[9], [26], [45], [46]). 28. Котельников А.П., Проективная теория векторов. Изв. Казанск. Фн -мат об-ва, 2- серия, 1892, VIII и IX 29. —, Винтовое счисление. Уч. зап. Казанск. ун-та, 1895—1896. Отд. изд. 1895 30. —, Принцип относительности и геометрия Лобачевского. В сб. «In memorial Lobatchevskii». Казань, 1927, 2, 37—66 31. Лобачевский Н.И., Собрание сочинений в 5 томах. Под ред. В.Ф. Кагана. М. —Л., Гостехиздат, 1949 58 - Черников Н.А., Распад частицы и соединение частиц в образах пространства скоростей. Научн. докл. высш. школы, физ.-мат. н., 1958, № 2, 158—161 (РЖМат, 1960, 859) 59 - Релятивистское распределение Максвелла — Больцмана и интегральная форма законов сохранения. Препринт (Объедин. ин- ядер, исслед., —723). Дубна, 1961 60 - Кинетическое уравнение для релятивистского газа в произвольном гравитационном поле. Препринт (Объедин. ин- ядер, исслед., Р—1028). Дубна, 1961 61 - Применение геометрии Лобачевского в специальной теории относительности. Междумар. зимняя школа теор. физики. Объедин. ин- ядер. исслед. Дубна, 1964 62 - Лекции по геометрии Лобачевского и теории относительности. Новосибирск. Гос. ун-т, 1965 63 — Стохастическое движение релятивистской частицы. Преприн (И1Ф, 68—44). Киев, 1968 64 - Геометрия Лобачевского и релятивистская механика. В сб. «Физика элементарных частиц и атомного ядра». М., Атомиздат, 1973, 4, вып. 3, 773—810 65 — Введение геометрии Лобачевского в механику. В сб. «Классическа и квантовая теория гравитации». Минск, Ин-т- физик А БССР, 1976, 47—53 66 — Геометрия Лобачевского как физическая наука. Препринт. (Объедин. ин- ядер, исслед., Р2—10251). Дубна, 1976 67 — Введение геометрии Лобачевского в механику. Препринт (Объедин. ин- ядер, исслед., Р2—9620). Дубна, 1976, 9 с. (РЖМат, 1976, 12А836) 68 — Геометрия Лобачевского как физическая наука. Всес. науч. конф. по неевклид. геометрии «150 лет геометрии Лобачевского», Казань, 1976. М., 1977, 146—153 (РЖМат, 1978, 7А943) С.Б. Кадомцев, Э.Г. Позняк, Д.Д. Соколов, Некоторые вопросы геометрии Лобачевского, связанные с физикой, Итоги науки и техн. Сер. Пробл. геом., 1982, том 13, 157–188 https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=intg&paperid=135&option_lang=rus ...Рассуждая совершенно так же, как и в случае движения точки по прямой или по плоскости, мы можем установить однозначное соответствие между скоростями и точками абсолюта, остающееся неизменным при переходе от одной системы отсчета к другой. При этом скоростям меньшим скорости света с будут соответствовать реальные точки абсолюта Л3, лежащие внутри поверхности S2, скоростям больших чем с, — точки идельные, и наконец скоростям равным скорости света — точки самой поверхности S2. Мы можем поверхность S2 назвать световой поверхностью или световым абсолютом пространства Лобачевского Л3 А.П. Котельников. Принцип относительности и Геометрия Лобачевского, In mem. Lobatschevskii, 1927, том 2, 37–66 https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=kumem&paperid=6&option_lang=rus |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5172
Зарегистрирован: 27.08.07
|
|

Отправлено: 10.03.23 15:10. Заголовок: Н.И. Лобачевский. По..
Н.И. Лобачевский. Полное собрание сочинений по геометрии  Первые понятия, с которых начинается какая-нибудь наука, должны быть ясны и приведены к самому меньшему числу. Тогда только они могут служить прочным и достаточным основанием учения. Такие понятия приобретаются чувствами; врожденным не должно верить (О началах геометрии. Полное собрание сочинений). Первыми данными, без сомнения, будут всегда те понятия, которые мы приобретаем в природе посредством наших чувств. Ум может и должен приводить их к самому меньшему числу, чтобы они служили потом твердым основанием в науке (Новые начала геометрии. с.231). В природе мы познаем собственно только движение, без которого чувственные впечатления невозможны. Все прочие понятия, напр., геометрические, произведены нашим умом искусственно, будучи взяты в свойствах движения, а потому пространство само собой отдельно для нас не существует. После чего в нашем уме не может быть никакого противоречия, когда мы допускаем, что некоторые силы в природе следуют одной, другие своей особой Геометрии (с.227) Н.И. Лобачевский. Полное собрание сочинений по геометрии. Том 1. Казань, 1883. 561с. http://books.e-heritage.ru/book/10070447 https://vk.com/doc-99389082_417758838 42мб pdf 3. 1829—1830. О началах геометрии ("Казанский Вестник", ч. 25, февраль и март 1829, стр. 178—187; апрель 1829, стр. 228—241; ч. 27, ноябрь и декабрь 1829, стр. 227—243, табл. I, фиг. 1—9; ч. 28, март и апрель 1830, стр. 251—283, табл. II, фиг. 10—17; июль и август 1830, стр. 571—636). Перепечатано в полном собрании сочинений по геометрии, т. I, Казань, 1883, стр. 1—67. 9. 1835. Воображаемая геометрия ("Ученые Записки", 1835, І, стр. 3—83, табл. с фиг. 1—8). Почти совпадает с № 13. Перепечатано в Полном собрании сочинений, т. І, стр. 71—120 11. 1835—1838. Новые начала геометрии с полною теориею параллельных ("Ученые Записки", 1835, III. стр. 3—48. Введение и глава І, І таблица, фиг. 1—20; 1836, II, стр. 3—98, главы IІ — V, 3 табл., фиг. 21—41, 42—60, 61—75; 1836, III, стр. 3—50, главы VI—VII, 2 табл., фиг. 76—91, 92—106; 1837, І. стр. 3—97, главы VIII—XI, 2 табл., фиг. 107—120, 121—134; 1838, І, стр. 3—124, глава XII; 1838, III, стр. 3—65, глава XIII). Перепечатано в Полном собрании сочинений, т. І, стр. 219—486 13. 1837. Géométrie imaginaire par М-r. N. Lobatschewsky, recteur de l'Université de Cazan. (Журнал Крелле. T. 17, тетр. 4, стр. 295—320, 1 табл., фиг. 1—8. Берлин, 1837; послано в 1834 или 1835 г.). Перепечатано в Полном собрании сочинен., т. II, стр. 581—613. https://runivers.ru/philosophy/lib/authors/author439275/ Первым, кто внес выдающийся вклад в пропаганду открытия Лобачевского и восстановление памяти о нем, был математик Александр Васильевич Васильев. Он был инициатором и главным организатором празднования в Казани в 1893г. столетия со дня рождения ученого. Васильев предложил создать «Библиотеку Лобачевского» («Bibliotheka Lobachevskiana»), издать полное собрание его трудов, учредить премию. О начальном этапе биографии ученого не были осведомлены даже современники. Наибольшая заслуга в деле освещения жизни и личности Лобачевского, а также увековечения его памяти принадлежит покойному профессору Казанского университета А.В. Васильеву. 22 октября 1893г. на торжественном собрании Казанского университета по поводу столетия со дня рождения Лобачевского он выступил с речью, положившей начало систематическому сбору материала о жизни и творчестве великого ученого. А.В. Васильев. "Н. И. Лобачевский". Речь, произнесенная в торжественном собрании Имп. Казанского университета 22 октября 1893г., Казань, 1894. 48с. https://runivers.ru/philosophy/lib/book8920/477503/ |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5173
Зарегистрирован: 27.08.07
|
|

Отправлено: 11.03.23 15:40. Заголовок: Геометрия Лобачевско..
Геометрия Лобачевского и релятивистская механика  Из Заключения - Н.И. Лобачевский. О началах геометрии (1829—1830) ...Оставалось бы изследовать, какого рода перемена произойдет от введения воображаемой Геометрии в Механику, и не встретится ли здесь принятых уже и несомнительных понятий о природе вещей, но которые принудят нас ограничивать, или совсем не допускать зависимости линии и углов. Однакож можно предвидеть, что перемены в Механике при новых началах Геометрии будут того же рода, как показал Лаплас (Mecanique celeste Т. I. Liv. I. Ch. II.), предполагая возможной всякую зависимость скорости от силы, или выразимся вернее — предполагая силы, измеряемые всегда скоростью, подчиненными другому закону в соединении, нежели принятому сложению их Н.И. Лобачевский. Полное собрание сочинений по геометрии. Том 1. Казань, 1883. 561с. http://books.e-heritage.ru/book/10070447 https://vk.com/doc-99389082_417758838 42мб pdf  Геометрия Лобачевского и релятивистская механика Н.А. Черников Объединенный институт ядерных исследований, Дубна Приводятся основные понятия и результаты геометрии Лобачевского. С точки зрения геометрии Лобачевского излагается механика. Введение Творец неевклидовой геометрии Н.И. Лобачевский, как известно, решил проблему параллельных, над которой так безуспешно трудились многие и многие поколения. О трудности этой проблемы можно судить по тому, что уже найденное ее решение было понято лишь немногими современниками великого ученого. Однако следующее поколение геометров овладело геометрией Лобачевского, почувствовало ее силу в точных науках и нашло простые способы ее изложения. За релятивистскую механику в физической аудитории агитировать не приходится: она является рабочим инструментом в физике высоких энергий. Но, применяя этот инструмент, не всегда знают, что в основном имеют дело с геометрией Лобачевского. А между тем — имеют, поскольку пространство скоростей в релятивистской механике является пространством Лобачевского. Незнание этого часто приводит к непроизводительной затрате сил и, разумеется, затрудняет понимание самой релятивистской механики. Открывать же каждый раз заново геометрию Лобачевского — дело трудное и, конечно, лавров уже не приносящее. Трудность выбранной темы обзора в том и состоит, что в большинстве своем физики не знакомы с геометрией Лобачевского. В связи с этим обзор разбит на две части. В первой, вспомогательной, части обзора излагается суть проблемы параллельных и история ее решения. Приводятся основные понятия и результаты геометрии Лобачевского. Раскрывается богатство стереометрии Лобачевского; содержащей на плоскости планиметрию Лобачевского, на сфере — сферическую планиметрию и, что наиболее замечательно, на орисфере —планиметрию Евклида. Приводимых в обзоре сведений из тригонометрии достаточно для решения большинства задач механики контактных столкновений. На основе тригонометрии выводятся формулы Лобачевского для угла параллельности и для зависимости площади круга и длины окружности от радиуса. Наконец, вводятся бельтрамиевы координаты, с помощью которых во второй части обзора определяется пространство скоростей. Во второй, главной, части обзора излагается релятивистская механика одной и двух частиц. Не останавливаясь на деталях, отметим следующие основные моменты. Если в пространстве скоростей частицы геометрию Евклида заменить геометрией Лобачевского, то преобразования Галилея заменятся на преобразования Лоренца. В этом случае в механике одной частицы происходят изменения, во всем аналогичные тем, которые происходят в геометрии при отрицании евклидова постулата о параллельных. Например, хотя кинетическая энергия и импульс частицы продолжают выражаться площадью круга и длиной окружности в пространстве скоростей, но сам вид зависимости этих величин от радиуса изменяется в соответствии с формулами Лобачевского. Более радикальным изменениям подвергается механика двух и более частиц. В этой обширной части механики остается неразрушенной только механика контактных столкновений. Последняя же изменяется в такой мере, в какой и механика одной частицы. Так, закон сохранения импульса при распаде одной частицы на две продолжает оставаться эквивалентным паре архимедовых законов рычага в пространстве скоростей. Однако вместо плеч в этих законах приходится считать длины окружностей, описываемых рычагами. Эквивалентность закона сохранения импульса паре законов рычага Архимеда позволяет представить релятивистскую механику контактных столкновений в виде статики в пространстве Лобачевского. С помощью такого рода представлений во второй части обзора решается ряд механических задач. Этим автор надеется показать практическую ценность излагаемого материала... Н.А. Черников. Геометрия Лобачевского и релятивистская механика // ЭЧАЯ. 1973. Т. 4, вып. 3. с.773-810 https://vk.com/s/v1/doc/ElVDcv6UcJLA1OX1X5PFSP70Gs_TRvTwbq0XJwR84EIFwKeEsUg |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5174
Зарегистрирован: 27.08.07
|
|

Отправлено: 12.03.23 14:11. Заголовок: Научное и научно-пед..
Научное и научно-педагогическое наследие А.П. Котельникова - заведующего кафедрой теоретической механики МВТУ им. Н.Э. Баумана (к 150-летию со дня рождения) # 12, декабрь 2015 Колесников К.С., Шкапов П.М., Панкратов А.А.  В высшем техническом образовании России дисциплина «Теоретическая механика» берёт начало с лекций Н.Е. Жуковского, которые он с 1878г. стал читать в Императорском московском техническом училище (ИМТУ) отдельно от курса математики. За 43 года руководства кафедрой теоретической механики сформированная нашим великим ученым-механиком, «отцом русской авиации», программа курса лекций по теоретической механики была дополнена введением практических занятий, демонстрацией механизмов из собираемой им коллекции приборов, итоговой аттестацией в виде экзамена с билетами, включающими задачи. Занятия со студентами проводили не только штатные сотрудники кафедры, но привлекались также ведущие профессора Московского университета, крупные ученые и инженеры. Таким образом, была не только сформирована фундаментальная инженерная дисциплина, но и создан коллектив, который под руководством профессора Н.Е. Жуковского в течение 43 лет успешно решал задачу подготовки высококлассных инженеров для работы в разных отраслях развивающейся промышленности России, включая машиностроение, металлообработку, энергетику, а также бурно развивающееся авиа- и двигателестроение, многие др. [1-3]. 17 марта 1921г. Н.Е. Жуковского не стало, и остро встал вопрос о его преемнике на должность заведующего кафедрой теоретической механики МВТУ им. Н.Э. Баумана (б. ИМТУ). Ученый совет пригласил на эту должность известного математика и механика Евгения Александровича Болотова, который ранее работал на кафедре и о научных работах которого Н.Е. Жуковский отзывался очень положительно. Занимавший в 1918-1920г.г. должность ректора Казанского университета и заведующего кафедрой теоретической и практической механики, Е.А. Болотов принял предложение Ученого совета возглавить кафедру теоретической механики МВТУ и в 1921г. переехал в Москву. Однако, менее чем через год, он скоропостижно умер, и вопрос о руководителе кафедры возник вновь. В 1924г. заведующим кафедрой был избран Александр Петрович Котельников, который был в то время ярким представителем Казанской школы математиков и механиков [2-4], рис. 1.  Рис. 1 А.П. Котельников - представитель Казанской школы механиков и математиков, 1896г. А.П. Котельников родился 8 (20) октября 1865 года в г. Казани в семье профессора Казанского университета Петра Ивановича Котельникова, коллеги и сподвижника Н.И. Лобачевского. Александр Котельников в 1883г. окончил гимназию с серебряной медалью и в том же году поступает в Санкт-Петербургский технологический институт, но в 1884г. переводится на математическое отделение физико-математического факультета Казанского университета. В 1893г., сдав магистерский экзамен по прикладной математике, он получил звание приват-доцента Казанского университета и стал читать курсы графической статики и теории упругости, вел со студентами упражнения по теоретической механике [4]. В 1896г. А.П. Котельников защитил магистерскую диссертацию под названием «Винтовое счисление и его приложение к геометрии и механике» [5]. В своей речи на защите диссертации, А.П. Котельников отмечал, что возрастающая сложность задач механики требует более сложных методов и указывал, что «...винт, как метод, имеет важное значение в вопросах теоретической механики, а именно в статике, кинематике и динамике твердого тела». Винтовое счисление» - математический аппарат, который с единых позиций описывает силовые винты (R, L0) и винтовые представления кинематики (V, О). Здесь R - главный вектор, а L0 - главный момент системы сил; V - скорость точки тела, а О - угловая скорость тела, рис.2.  Рис. 2. Винты в теоретической механике: а) динамический винт; б) кинематический винт Каждый из этих винтов характеризуется совокупностью двух векторов: одного вектора свободного и одного вектора скользящего. Совокупность этих двух векторов Котельников назвал бивектором. Созданная им теория включала действия над бивекторами и возможность анализа механического движения по их изменениям. Если векторное произведение двух векторов дает кватернион, то произведение двух бивекторов дает бикватернион (термин английского математика Клиффорда). Затем А.П. Котельников развивает аналитическую теорию параболического бикватерниона в евклидовом пространстве. Здесь он вводит новую комплексную единицу w, причем w^2 = 0 и делает вывод, что произведение бивектора b на бивектор a есть бикватернион q = g0+ wg1, где g0 и g1 есть кватернионы. Котельников вводит весьма важное для теории понятие о комплексном угле между двумя прямыми в пространстве. Благодаря этому, операции над бивекторами получают с внешней стороны вид, тождественный с тем, который имеют операции над векторами в теории кватернионов. И дальше А.П. Котельников приходит к заключению, что между построениями и теоремами теории векторов и построениями и теоремами теории винтов можно провести полнейший параллелизм, так что каждому построению и теореме теории векторов будет отвечать построение и теорема теории винтов: формулы, выражающие соответствующие теоремы, будут одним и те же. «Все операции, которые мы совершаем над кватернионами, можно совершать над бикватернионами, все формулы теории кватернионов можно рассматривать как формулы теории бикватернионов. Однако геометрический смысл операций над кватернионами и бикватернионами различен. Операциям над кватернионами соответствуют построения теории векторов, имеющих общее начало, а операциям над бикватернионами - построения теории винтов» [5]. В своих научных исследованиях А.П. Котельников (как и его отец - профессор Казанского университета П.И. Котельников) поддерживал и развивал фундаментальные идеи Н.И. Лобачевского. Еще до защиты магистерской диссертации у него возник замысел распространения винтового исчисления на неевклидовы пространства. Так, перед защитой магистерской диссертации им были опубликованы тезисы («Положения»), в которых он писал: «Изучение механики неевклидовых пространств заслуживает самого серьёзного внимания во многих отношениях. Вопрос о роде нашего пространства едва ли может быть решён прежде, чем будет разработана механика пространств неевклидовых». Развитие этих идей и было реализовано в докторской диссертации А.П. Котельникова. В 1899г. А.П. Котельников публикует работу «Проективная теория векторов» [6], посвященную обобщению винтового исчисления на неевклидовы пространства. Эта работа была представлена им в качестве диссертации на соискание ученой степени доктора прикладной математики и успешно защищена в Казанском университете 23 мая 1899г. Причем, признавая особо выдающееся значение диссертации, А.П. Котельникову присвоили сразу две ученых степени: степень доктора чистой математики и степень доктора прикладной математики. В опубликованных позднее работах [7,8] также указывалось на важность обобщения векторного исчисления и построенного на его основе винтового исчисления для неевклидовых пространств постоянной кривизны - пространств Лобачевского и Римана. В 1899 году А.П. Котельников избирается заведующим кафедрой теоретической механики Киевского политехнического института (КПИ), где в течение четырех лет читал основной курс теоретической механики на механическом и химическом отделениях. В 1903г. А.П. Котельникова приглашается на кафедру чистой математики Казанского университета, избирается на должность заведующего кафедрой, и с 1904 по 1914гг. читает там лекции по аналитической геометрии, высшей алгебре и дифференциальному исчислению. Одновременно он продолжал активно вести научные исследования в области геометрии и механики, специальной теории относительности. С 1910г. Александр Петрович становится деканом физико-математического факультета Казанского университета. В 1914 г. А.П. Котельников возвращается в Киев, где преподает на кафедре математики Киевского университета, читает лекции по сферической тригонометрии, начертательной геометрии и дифференциальной геометрии. Он также ведет занятия по математике на Киевских высших женских курсах, а с 1920 по 1924г. вновь заведует кафедрой теоретической механики в КПИ [4]. В 1924г. в связи с избранием по конкурсу А. П. Котельников стал заведовать кафедрой теоретической механики Московского высшего технического училища им. Н.Э. Баумана. Возглавив кафедру, А.П. Котельников активно приступил к перестройке методической работы на кафедре, пересмотру содержания курса и написанию учебных пособий. Он активно поддержал предложение по векторному изложению курса теоретической механики для студентов. Инициатором этого выступил известный ученый-механик А.И. Некрасов, который, не прерывая связи с МВТУ, стал впоследствии заведующим кафедрой теоретической механики мехмата МГУ, академиком АН СССР. Будучи заведующим кафедрой теоретической механики, Александр Петрович Котельников также читал в МВТУ лекции по математике, вел курс теоретической механики и в других московских втузах: в институте инженеров транспорта (МИИТ) с 1924 по 1930гг.; в химико-технологическом институте (МХТИ) с 1926 по 1930гг., в лесотехническом институте с 1929 по 1930гг., в энергетическом институте (МЭИ) с 1933 по 1940гг. В 1929г. Котельников читал лекции по теоретической механике в Воскресном университете при МВТУ, а в 1930-1933гг. был одним из организаторов Высших инженерно-педагогических курсов для подготовки преподавателей втузов, где также читал курс теоретической механики. В 1925г. был опубликован учебник А.П. Котельникова «Введение в теоретическую механику» [9]. Это было одно из первых учебное пособий для студентов высших технических учебных заведений России. В 1927г. А.П. Котельников опубликовал большую работу «Точки Бурместера, их свойства и построение» [10], относящуюся к кинематике плоских механизмов. Точки Бурместера имеют важное значение при построении приближенных направляющих механизмов. В том же году в «Трудах МММИ им. Н.Э. Баумана» А.П. Котельников опубликовал работу «Заметки по графической динамике», в которой автор устанавливает теоремы, связывающие ускорения точек твердого тела в плоскопараллельном движении с силами, приложенными к телу. Эти теоремы приводят к простым методам графического определения реакций связей и решению ряда других задач динамики. В работе он дает ряд геометрических построений, позволяющих чисто графическим путем решать самые разнообразные задачи динамики. В 1939г. издательство МВТУ выпустило книгу «Теория гироскопов» [11], представляющую собой конспект лекций А.П. Котельникова, прочитанных в МВТУ. По отзывам специалистов и студентов в этих лекциях изложение материала отличалось предельной ясностью. Несмотря на небольшой объем, эта книга содержала обширный материал по вопросам кинематики и динамики твердого тела с одной неподвижной точкой и некоторые их приложения. Все изложенные в книге темы в своей совокупности образуют стройную теорию гироскопов. Она не утратила своего значения и в настоящее время, будучи особенно полезной для студентов и механических и приборостроительных факультетов. К сожалению, эта книга стала библиографической редкостью. Кроме собственных научных исследований и научно-методических изысканий огромную подвижническую работу А.П. Котельников провел по редакторской подготовке издания Полного собрания сочинений Н.Е. Жуковского (в 8 томах). При этом он не ограничивался только редактированием законченных работ, а также разбирал черновые наброски Н.Е. Жуковского и публиковал их со многими приложениями в изданиях ЦАГИ (например, работа «Действие волнующейся жидкости малой глубины на плавающие на ее поверхности тела»). Столь же скрупулезно он занимался подготовкой издания Полного собрания сочинений Н.И. Лобачевского (в 5 томах). Комментируя мемуары Н.И. Лобачевского «О началах геометрии», помещенные в 1-м томе Полного собрания его сочинений, А.П. Котельников довел до конца ряд вычислений сложных определенных интегралов, значения которых указаны Лобачевским без вывода. Значение научных достижений А.П. Котельникова при его жизни не было раскрыто полностью: их истинное значение устанавливает настоящее и будущее. Главным достижением А.П. Котельникова остается его «винтовое счисление». Актуальность применения теории винтов и винтового исчисления постоянно растет с переходом исследователей от рассмотрения одноконтурных механизмов с одной степенью свободы к открытым кинематическим цепям манипуляторов и роботов, и далее к многоконтурным пространственным манипуляционным механизмам параллельной структуры [12-15].  Рис.3 А.П. Котельников - заведующий кафедрой теоретической механики МВТУ им. Н.Э. Баумана, 1943г. Выдающийся российский математик и механик, доктор наук, профессор, заслуженный деятель науки и техники РСФСР (1934), лауреат Государственной (Сталинской) премии (1943) Александр Петрович Котельников (1865-1944), рис.3, оставил глубокий след в математике и механике, обогатив методику их преподавания новыми идеями и подходами. На кафедре теоретической механики МГТУ им. Н.Э. Баумана бережно сохраняется память о выдающихся ученых и педагогах, преподававших теоретическую механику и руководивших кафедрой, созданной Николаем Егоровичем Жуковским [16]. Заложенный ими высокий научно-методический уровень преподавания механики, позволяет и в настоящее время формировать базовые знания выпускников Московского государственного технического университета им. Н.Э. Баумана (Национального исследовательского университета) на уровне современных требований науки, техники и производства. Список литературы 1. Колесников К.С. Николай Егорович Жуковский и Императорское московское техническое училище (МГТУ им. Н.Э. Баумана) // Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 1996. № 4. С. 5-19. 2. Научные школы МГТУ им. Н.Э. Баумана. История развития / под ред. И.Б. Федорова, К.С. Колесникова. 2-е изд., доп. М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. 464 с. 3. Дубинин В.В., Гатауллина Г.И., Назаренко Б.П. Кафедра «Теоретическая механика». Основные этапы развития (1878-2003). М.: Экскриблис-Пресс, 2003. 192 с. 4. Путята Т.В., Лаптев Б.Л., Розенфельд Б.А., Фрадлин Б.Н. Александр Петрович Котельников. М.: Наука, 1968, 122 с. 5. Котельников А.П. Винтовое счисление и некоторые приложения его к геометрии и механике (магистерская диссертация). Казань, 1895. 215 с. 6. Котельников А.П. Проективная теория векторов (докторская диссертация). Казань, 1899. 317 с. 7. Котельников А.П. Принцип относительности и геометрия Лобачевского // In memoriam Lobatschevskii: сб. ст. Т. 2. Казань, 1927. С. 37-66. 8. Котельников А.П., Фок В.А. Некоторые применения идей Лобачевского в механике и физике. М.; Л.: ГИТТЛ, 1950. С. 7-47. 9. Котельников А.П. Введение в теоретическую механику. М.; Л.: ОНТИ, 1925. 263 с. 10. Котельников А.П. Точки Бурместера, их свойства и построение // Математический сборник. 1927. Т. 34, № 3-4. С. 207-348. 11. Котельников А.П. Теория гироскопов. М.: МММИ им. Н.Э. Баумана, 1939. 128 с. 12. Диментберг Ф.М. Винтовое исчисление. М.: Наука, 1965. 199 с. 13. Диментберг Ф.М. Теория винтов и ее приложения. М.: Наука, 1978. 327 с. 14. Глазунов В.А., Костерева С.Д., Данилин П.О., Ласточкин А.Б. Применение винтового исчисления в современной теории механизмов // Вестник научно-технического развития. 2010. № 6. С. 12-17. Режим доступа: http://www.vntr.ru/nomera/2010-634/ (дата обращения 01.11.2015). 15. Гебель Е.С., Абдираимов А.А., Солонин Е.В. Кинематика четырехзвенных пространственных ползунных механизмов // Омский научный вестник. 2015. № 140. С. 49-54. 16. Кафедра «Теоретическая механика» имени профессора Н.Е. Жуковского: офиц. сайт. Режим доступа: http://fn.bmstu.ru/index.php/fn3 (дата обращения 12.12.2015). https://cyberleninka.ru/article/n/nauchnoe-i-nauchno-pedagogicheskoe-nasledie-a-p-kotelnikova-zaveduyuschego-kafedroy-teoreticheskoy-mehaniki-mvtu-im-n-e-baumana-k-150 |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5175
Зарегистрирован: 27.08.07
|
|

Отправлено: 12.03.23 23:47. Заголовок: А.П. Котельников и т..
А.П. Котельников и теория векторов в неевклидовых пространствах Большие заслуги в разработке проблем неевклидовой геометрии и механики принадлежали Александру Петровичу Котельникову (20 октября 1850 — 6 марта 1944), сыну П.И. Котельникова и ученику А.В. Васильева и Ф.М. Суворова. Вскоре после окончания Казанского университета (1889) Котельников приступил к разработке проблем механики неевклидовых пространств, результатом чего и явились его магистерская диссертация «Винтовое счисление и некоторые его применения к геометрии и механике» (Казань, 1895), а затем и докторская диссертация «Проективная теория векторов». В 1893—1899гг. он преподавал в Казанском университете в звании приват-доцепта. После защиты второй диссертации, за которую ему присудили степени доктора чистой и прикладной математики, Котельников некоторое время работал профессором в Киевском политехническом институте, с 1904 по 1914г — в Казани, затем в течение 10 лет вновь в Киеве (в университете и в Политехническом институте). С 1924г. и до конца жизни он руководил кафедрой механики в Московском Высшем техническом училище, преподавал и в других втузах и работал в ЦАГИ. Продолжая научные работы по механике и геометрии, он вместе с тем принял деятельное участие в подготовке Полного собрания сочинении Н.И. Лобачевского, а также, в качестве главного редактора, Полного собрания сочинений Н.Е. Жуковского. В 1934г. ему было присвоено звание заслуженного деятеля науки и техники РСФСР. В самом конце шестидесятых годов XIX века итальянский математик А. Дженокки и бельгиец Ж. де Тилли занялись вопросами неевклидовой механики, на необходимость разработки которой указывал еще сам Лобачевский. Правда, первоначальной целью обоих авторов была попытка доказать от противного евклидов постулат о параллельных, получив при отказе от этого постулата какое-либо противоречие в системе механики. Но противоречие такого рода, естественно, не обнаруживалось, и, убедившись в тщетности поисков, Дженокки и де Тилли положили начало неевклидовой механике. Проблема привлекла внимание ряда ученых. В России первые работы по этому вопросу принадлежали А.П. Котельникову и Павлу Соломоновичу Юшкевичу (11 июля 1873 — 6 декабря 1943), опубликовавшему работу «О сложении сил в гиперболическом пространстве» (Вести, опытной физики и элем, математики, сем. 22, 1898). Сложение сил, скоростей, вообще векторов в евклидовом пространстве выражается правилом параллелограмма. В пространстве Лобачевского параллелограммов нет и необходимо иное определение векторной суммы. Проблема сложения векторов в пространствах постоянной кривизны явилась одним из отправных пунктов творчества А.П. Котельникова. Во введении к докторской диссертации он, характеризуя наиболее существенные пункты, отличающие ее от работ других авторов, указывал, во-первых, что рассматривает кинематику и динамику твердого тела не по отдельности, но соединяет их в одну более отвлеченную теорию векторов, и, во-вторых, что «все указанные мною авторы задавали силу и скорость совокупностью прямой и числа, и только де Тилли и П. Юшкевич изобразили силы и скорость им пропорциональными отрезками прямой. Такое геометрическое представление у названных авторов, однако, не играет никакой существенной роли, и даже простейшим законом сложения сил и скоростей эти авторы, подобно всем другим, пользовались в его аналитической форме. Никто, насколько мне известно, не задавался вопросом, не следует ли, изображая силы и скорости прямолинейным отрезком, принять какую-нибудь другую зависимость между длиной этих отрезков и величиной изображаемых ими сил и скоростей вместо прямой пропорциональности, никто не задавался вопросом, нельзя ли основной закон механики — закон сложения сил и скоростей выразить в столь же простой геометрической форме, как и правило параллелограмма в евклидовом пространстве и, таким образом, придать механике твердого тела в неевклидовых пространствах более геометрический характер. Эти вопросы следует считать исходными вопросами моей работы. Они повели меня в свою очередь к более глубокому анализу тех предположений, которые необходимы с точки зрения проективной геометрии для формального обоснования теории векторов» (А.П. Котельников. Проективная теория векторов. Введение к докторской диссертации (отд. оттиск). Казань, 1899, стр. 29.). Построение теории векторов с приложениями к механике и геометрии и составляет содержание обеих диссертаций А.П. Котельникова, причем основным аппаратом служит винтовое исчисление и арифметика особого рода комплексных чисел с двумя единицами. Корни винтового исчисления восходят к теории кватернионов Гамильтона, о которой нам еще придется говорить (см. стр. 555 и след.), и развивающим ее трудам У. Клиффорда и Р. Болла, которые начали появляться в семидесятые годы XIX века. Были введены общие комплексные числа вида а + bw, где вторая единица w для пространств Евклида, Римана и Лобачевского определяется соответственно равенствами w^2=0, w^2=k^2>0, w^2=k^2<0 (k^2 — кривизна пространства). Эти числа были названы, следуя тому же порядку, параболическими, эллиптическими и гиперболическими; частным случаем последних являются обыкновенные комплексные числа, k^2 = —1. Выражения q1 + wg2, в которых g1, и g2 - суть гамильтоновы кватернионы, именуются бикватернионами и последние, подобно общим комплексным числам a + bw, подразделяются на параболические, эллиптические и гиперболические. Для характеристики системы приложенных к телу сил и его движения в пространстве Евклида было предложено понятие винта, как пары скользящего и свободного векторов, которые можно выбрать коллинеарными. Между всеми тремя категориями объектов существует тесная взаимосвязь: параболический кватернион можно рассматривать как сумму параболического комплексного числа и винта. В свою очередь винт, определяемый скользящим вектором r и свободным вектором r', есть комплексный вектор r + wr’. В случае пространства постоянной ненулевой кривизны систему приложенных сил можно заменить двумя скользящими векторами, направленными по двум взаимно полярным прямым. Такой винт получил название мотора (Дело в том, что мОтор характеризует произвольное движение (лат motio) в рассматриваемом пространстве. Напомним, что вектор характеризует перемещение (лат. vectio) вдоль прямой). Только что указанные связи между бикватернионами, общими комплексными числами, винтами и векторами имеют место и для моторов. Заметим еще, что вторая единица общего комплексного числа w является оператором некоторого преобразования вектора, на который умножается w. Двукратное применение этой операции в евклидовом пространстве дает нуль-вектор, так что w^2 = 0; вообще же w^2 = k^2. Магистерская диссертация А.П. Котельникова, предметом которой служили векторы, винты и их приложения для случая пространства Евклида, явилась как бы вступлением к докторской. В «Проективной теории векторов» дана общая теория векторов пространств постоянной кривизны, трактуемых как метрические проективные пространства. Метризация, т.е. измерение длин и углов, достигается тем, что в рассматриваемом проективном пространстве фиксируется так называемый абсолют — действительная или мнимая поверхность второго порядка, которая переходит сама в себя при проективном преобразовании, переводящем точки, лежащие на одной прямой, в точки, расположенные опять-таки на прямой. Для пространства Евклида абсолют есть бесконечно удаленная плоскость вместе с принадлежащей ей мнимой линией пересечения всех сфер, для пространства Римана — некоторая мнимая поверхность и для пространства Лобачевского — поверхность замкнутая. В докторской диссертации подробно изложены арифметика общих комплексных чисел, учение об их элементарных функциях и геометрические интерпретации на плоскости и поверхностях второго порядка. Далее последовательно разрабатывается теория векторов и операции над ними. 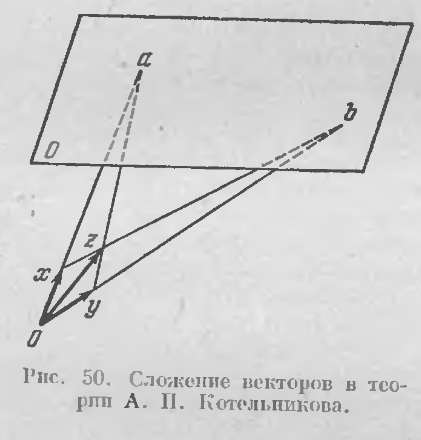 Сложение производится по правилу четырехугольника: на рис.50 сумма векторов ох и оу определяется как диагональ oz; следует иметь в виду, что точки a и b находятся в пересечении прямых, несущих ох и оу с плоскостью О, полярной с точкой о относительно абсолюта. В пространстве Евклида плоскость О бесконечно удаленная и четырехугольник переходит в параллелограмм. Для векторов, мОторов и еще третьего вида основные объектов роторов, которые вводятся как пары плоскостей, пересечение которых называется осью ротора (Мотор характеризует вращение -лат. rotation - тела около оси. Заметим, что мотор можно вводить и как пару, составленную из вектора и ротора с осью, проходящей через начало вектора. Всякое движение в рассматриваемых пространствах можно в любой момент рассматривать как перемещение вдоль прямой, вместе с вращением вокруг нее), определяются различные характеризующие их величины, которые, так же как и операции над ними, во многом сходны со свойствами обыкновенных векторов и служат их обобщениями. Все это осуществляется с помощью исчисления бикватернионов, которые Котельников предпочитает рассматривать не в форме q1 + wg2, а в форме q = w + ix + jy + kz, где w, х, у, z - суть общие комплексные числа a + bw. Это позволяет весьма просто переводить формулы теории кватернионов в формулы теории бикватернионов и, на основе сходства обеих теорий, установить параллелизм геометрических систем, которые служат их геометрической интерпретацией, т.е. теории векторов и теории моторов. В более поздней работе, опубликованной уже посмертно, А.П. Котельников писал: «Мы приходим, таким образом, к мысли перенести из теории векторов такие элементарные понятия, как длина вектора, проекция вектора, координаты вектора, угол между двумя векторами и т.д. в теорию моторов и внести в эту последнюю соответствующие понятия: тензор мотора, проекции мотора, комплексные координаты мотора, комплексный угол между прямыми и т.д. (Тензор мотора, определяемого парой скользящих векторов с углом ф между ними и кратчайшим расстоянием d, есть комплексное число tg(ф) + w/k tg(kd); комплексным углом между двумя прямыми называется число ф + wd; проекция мотора на ось равна произведению его тензора на косинус комплексного угла между осью мотора и осью проекции). Вместе с тем получается возможность каждому построению и теореме теории связки векторов сопоставить построение и теорему теории моторов и, пользуясь первыми, находить новые еще не известные теоремы теории моторов. Таким образом, мы приводим к принципу перенесения» (А.П. Котельников. Теория векторов и комплексные числа. В кн.: А.П. Котельников. В.А. Фок. Некоторые применения идей Лобачевского в механике и физике. М.-Л., 1950, стр.42). Принцип перенесения имеет большое значение в исследовании Котельникова, устанавливая соответствие между простыми геометрическими фигурами и более сложными. Если взять комплексную сферу единичного радиуса в евклидовом пространстве, координаты которого суть общие комплексные числа a + bw, то один из основных результатов А.П. Котельникова можно высказать следующим образом: множество лучей неевклидова пространства взаимно однозначно изображаются комплексной сферой, причем комплексный угол между прямыми равен сферическому расстоянию соответственных точек сферы, а щетки прямых (множества перпендикуляров к одной прямой) изображаются большими кругами сферы. Вместе с тем, движения неевклидова пространства изображаются вращениями комплексной сферы, и обратно. Исследования Котельникова развивались одновременно с аналогичными изысканиями немецкого математика Э. Штуди, начатыми в 1891г. и завершенными в наиболее важных частях в 1899—1901гг. (Б.А. Розенфельд, Александр Петрович Котельников,— Ист.-матем. исслед., вып. IX, 1956). Так в той же Казани, где Лобачевский положил начало неевклидовой геометрии, в широком плане была разработана теория векторов и механика трехмерных пространств постоянной кривизны. Неевклидова механика привлекала внимание и других русских ученых, помимо названных. Укажем для примера статью Н.Е. Жуковского «О движении материальной псевдосферической фигуры по поверхности псевдосферы» (1902) (Н.Е. Жуковский, Собрание сочинений, т.1, М.-Л. 1948. Юшкевич А.П. История математики в России до 1917 года. - М.: Наука, 1968. - 592с.) http://pyrkov-professor.ru/default.aspx?tabid=186&ArticleId=631 |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5176
Зарегистрирован: 27.08.07
|
|

Отправлено: 13.03.23 18:56. Заголовок: Принцип относительно..
Принцип относительности и Геометрия Лобачевского А.П. Котельников (Москва)  §1. Уже в первых работах, посвященных принципу относительности и появившихся вскоре после знаменитого мемуара Einstein'a «Zur Elektrodynamik bewegter Korper», мы находим намеки на то, что Геометрия Лобачевского при изложении этого принципа и при решении выдвинутых им проблем может оказаться весьма полезной. Так Н. Minkowski в своем классическом мемуаре: «Die Grundgleichungen für die elektromagnetische Vorgange in bewegten Korper», доказывая ковариантность ур. Maxwell'a–Hertz'a для Лоренцова преобразования, представляет это последнее как вращение на мнимый угол в плоскости x, t и полагает при этом v/c = g = i tg iψ = th ψ, т.е. выражает скорость при помощи гиперболического тангенса. Воспользовавшись этим выражением скорости, A. Sommerfeld показывает, что теорема сложения скоростей Einstein'a может быть весьма просто представлена треугольником сферы с мнимым радиусом. «Но», говорит Dr. V. Varićak, «гиперболическая геометрия есть мнимое отображение сферической, как это уже знали Лобачевский и Bolyai», и таким образом замечание A. Sommerfeld'a приводит к мысли о возможности применения Геометрии Лобачевского к принципу относительности. G. Herglotz пользуясь простейшими фактами неевклидовой Геометрии, которая, говорит он: «вообще в вопросах принципа относительности, напр. при сложении скоростей, может быть весьма полезна», для того, чтобы найти все возможные, согласные с принципом относительности движения твердого тела, т.е. для решения задачи, формулированной, но не вполне решенной М. Born'ом. Ряд аналогий между Геометрией Лобачевского и принципом относительности, замечание A. Sommerfeld'a и подстановка Г. Минковского v/c = th ψ натолкнули V. Varićak'a на мысль о неевклидовом истолковании принципа относительности. Результаты своих исследований он формулирует таким образом: «если положить в основу неевклидову терминологию, то не только существенным образом упрощаются формулы теории относительности, но они допускают также геометрическое истолкование, совершенно аналогичное интерпретации классической теории в Евклидовой Геометрии. И эта аналогия простирается местами так далеко, что можно оставить неизменной и словесную формулировку теорем с той лишь разницей, что надо заменить Евклидовы образы соответственными образами пространства Лобачевского с параметром с = 3·1010 сант.». В своих многочисленных заметках и мемуарах V. Varićak дает много примеров, иллюстрирующих его мысль: при помощи построений в пространстве Лобачевского он весьма просто представляет закон сложения скоростей Einstein'a, принцип Doppler'a, аберрацию света, отражение света от движущегося зеркала и т.д. В прекрасном мемуаре «О геометрических основаниях Лоренцовой группы» F. Klein показав, что группа Лоренцовских преобразований есть проективная группа, оставляющая инвариантной квадратичную форму x^2 + y^2 + z^2 – c^2* t^2, тем самым устанавливает связь ее с группой преобразований пространства Лобачевского. §2. Таким образом, благодаря указанным работам математиков, обнаружилось, что Геометрия Лобачевского, которая до сих пор не имела никакого значения для физических теорий, должна играть важную роль в специальном принципе относительности. Это обстоятельство может показаться несколько странным, ибо различие между механикой Einstein'a и механикой Ньютона заключается только в том, что в первой скорость света считается абсолютно постоянной, но как в той, так и в другой предполагается, что явления окружающей нас природы происходят в пространстве Евклида. Естественно возникает вопрос: почему же, несмотря на то, что в основание как механики Einstein'a, так и механики Ньютона положено пространство Евклида, до сих пор при изучении классической механики, на протяжении столетий, никогда не ощущалось потребности ни в каких других геометрических построениях, кроме тех, которым учит нас Геометрия Евклида, между тем как не прошло и пяти лет после опубликования мемуара Einstein'a, как появились вполне определенные указания на то, что Геометрия Лобачевского является весьма подходящим орудием для изучения механики Einstein'a? Мы получим ответ на этот вопрос, если, с одной стороны, обратимся к той изящной геометрической интерпретации, которую ввел в принцип относительности Г. Минковский, а с другой воспользуемся проективной Геометрией и теорией мероопределения, развитой A. Cayley и F. Klein'ом в их классических мемуарах. Пусть x, y, z, обозначают прямоугольные координаты пространства, а t – время. «Предметом нашего восприятия», говорит Г. Минковский, «являются всегда места и времена, связанные между собой. Никто не замечал места иначе как в определенное время, и не замечал времени иначе как в определенном месте». Назовем систему значений x, y, z, t «мировой точкой». Многообразие всех мыслимых мировых точек x, y, z, t Г. Минковский называет «миром». Мир Г. Минковского это пространство четырех измерений. Какова же структура этого пространства? Будет ли оно пространством постоянной кривизны, и если оно постоянной кривизны, то принадлежит ли оно к типу пространств Евклида, Римана или Лобачевского? Сказанное мною выше о значении Геометрии Лобачевского для принципа относительности может, пожалуй, внушить мысль, что этот мир Минковского и есть пространство Лобачевского. Такая догадка была бы, однако, несколько поспешной: мир Минковского – это пространство Евклида, но только особого вида. Как в нашем обыкновенном Евклидовом пространстве могут быть поверхности постоянной положительной, отрицательной или нулевой кривизны, так и в мире Минковского 4-х измерений могут быть построены 3-х мерные пространства любой постоянной кривизны, и то пространство Лобачевского, которое играет такую выдающуюся роль в принципе относительности, должно находиться где-то в 4-хмерном мире Г. Минковского. Но где же именно? Чтобы ответить на этот вопрос, мы должны припомнить некоторые основные положения теории мероопределения. §3. С начала XVII столетия, со времени появления Геометрии Декарта, преобладающее значение получила Аналитическая Геометрия, которая позволяла все свойства фигур, будут ли то свойства метрические или проективные, изучать при помощи Декартова метода координат. Этот метод, благодаря его универсальности и могуществу, привлек к себе внимание геометров и, опираясь на основные метрические понятия, давал возможность положить их в основание всей геометрии. Отодвинув т.о. на задний план изучение проективных свойств фигур, Аналитическая геометрия расширила наши геометрические представления введением понятия о мнимых точках, линиях и поверхностях и подготовила почву для дальнейшего развития проективной Геометрии. Мало по малу проективные свойства фигур снова стали привлекать к себе внимание геометров; их значение в геометрии увеличивалось всё более и более, пока, наконец, во второй половине прошлого столетия взгляд на роль в геометрии метрических и проективных свойств не изменился. В эту эпоху стало совершенно ясно, что подобно тому, как Декартова Геометрия дает возможность свести все свойства фигур к свойствам метрическим, так проективная дает возможность проективные свойства положить в основание всей геометрии. Но при этом обнаружилось, что, изучая с точки зрения проективной геометрии метрические свойства какой либо фигуры, мы должны вместе с ней рассматривать еще и другую фигуру постоянную, неизменную, неподвижную, одну и ту же во всех случаях, которую называют абсолютом. Исключительно абсолютом обусловливаются метрические свойства пространства. Постараюсь объяснить, что служит абсолютом Евклидова пространства. Давно уже было замечено, что многие, по-видимому различные, теоремы Геометрии, становятся тожественными, делаются видоизменениями одной и той же теоремы, если мы будем представлять себе, что параллельные между собой линии все сходятся в одной и той же бесконечно удаленной точке, и будем считать, что все бесконечно удаленные точки одной и той же плоскости лежат на одной и той же бесконечно удаленной прямой линии и все бесконечно удаленные точки пространства образуют бесконечно удаленную плоскость. При такой точке зрения на каждой прямой линии есть только одна бесконечно удаленная точка, в которой она пересекает бесконечно удаленную плоскость. Основное метрическое понятие, связанное с прямой линией, расстояние между двумя ее точками, рассматривается в проективной геометрии как свойство фигуры, образованной тремя точками: двумя данными и бесконечно удаленной точкой прямой. Эта последняя и образует абсолют прямой линии Евклидова пространства. Далее геометры обратили внимание на то, что разнообразные кривые, которые мы получаем, рассекая поверхность круглого конуса плоскостью, так наз. конические сечения, легко поддаются простой классификации, если мы воспользуемся бесконечно удаленной прямой плоскости. Дело в том, что со всякой прямой, в том числе и с бесконечно удаленной, всякое коническое сечение пересекается в двух точках, но эти две точки могут быть различны, могут сливаться в одну, когда прямая касается конического сечения, и, наконец, будут мнимы, когда прямая с коническим сечением вовсе не встречается. Если коническое сечение пересекается с бесконечно удаленной прямой в двух действительных точках, то оно имеет вид гиперболы, если оно встречается с бесконечно удаленной прямой в двух совпадающих точках, т.е. касается с ней, то оно обращается в параболу. Наконец коническое сечение третьего типа, эллипс, пересекается с бесконечно удаленной прямой в двух мнимых точках. Круг есть частный случай эллипса, и мы должны, следовательно, сказать, что и он пересекается с бесконечно удаленной прямой в двух мнимых точках. Ряд геометрических фактов заставляет нас считать, что все круги плоскости пересекают бесконечно удаленную прямую в одних и тех же двух мнимых точках, которые и принято называть поэтому круговыми точками. Работы французской школы геометров первой половины прошлого столетия выяснили, что основные метрические понятия плоскости самым тесным образом связаны с бесконечно удаленной прямой и мнимыми круговыми точками на ней. Расстояние между двумя точками A и В, угол между двумя прямыми l и m рассматриваются в проективной геометрии как свойства тех фигур, которые мы получим, присоединив к точкам A и B, или к прямым l и m круговые точки. Эти последние вместе с бесконечно удаленной прямой и образуют абсолют Евклидовой плоскости. Подобным же образом оказалось, что при изучении геометрии трехмерного пространства полезно представлять себе, что все шаровые поверхности пересекаются с бесконечно удаленной плоскостью по одному и тому же мнимому кругу, который поэтому называют шаровым кругом. С точки зрения проективной геометрии метрические свойства какой-либо фигуры суть свойства сложной фигуры, составленной из нее и шарового круга. Этот круг вместе с бесконечно удаленной плоскостью, в которой он лежит, и служат абсолютом Евклидова пространства трех измерений. §4. Дальнейший шаг в развитии этих идей был сделан английским математиком A. Cayley. Он дал по его словам «теорию расстояний» или, как принято теперь говорить, «теорию мероопределения». Эта теория заключается в том, что мы можем, вводя основные метрические понятия, взять за абсолют прямой линии не одну точку, а две, за абсолют плоскости не бесконечно удаленную прямую с круговыми точками на ней, а любое коническое сечение. Обобщенная таким образом геометрия прямой линии обращается в геометрию Евклидовой прямой, когда две точки абсолюта сливаются в одну. Обобщенная же геометрия плоскости превращается в геометрию Евклидовой плоскости или в геометрию сферы, если коническое сечение, принятое за абсолют, обращается в пару круговых точек или становится мнимым. Сам A. Cayley, набросав в своем мемуаре на нескольких страницах теорию мероопределения, не останавливается на дальнейшем ее развитии и не касается следствий, из нее вытекающих. А между тем эти следствия имеют весьма большое значение для всей Геометрии. Первым, обратившим внимание на значение небольшого мемуара A. Cayley, был F. Klein. Упростив математическую сторону теории мероопределения, F. Klein показывает, что не только Геометрия Евклида и Геометрия сферы, но и Геометрия Римана и Лобачевского укладываются в геометрическую схему A. Cayley. Всё различие геометрии плоскости Евклида, Римана и Лобачевского обусловливается различием абсолютов этих трех типов плоскостей. Мы уже видели, что абсолютом Евклидовой плоскости служит прямая с двумя мнимыми точками на ней. Если же за абсолют мы примем коническое сечение, то получим плоскость Римана, когда оно будет мнимым, и плоскости Лобачевского, когда оно – действительно. Теория мероопределения A. Cayley может быть распространена и на пространство трех измерений. Если мы за абсолют примем не шаровой круг, а поверхность второго порядка, то получим или Геометрию Лобачевского, или Геометрию Римана, смотря по тому, будет ли поверхность действительной или мнимой. Надо однако заметить, что теория мероопределения дает возможность не только просто классифицировать уже хорошо изученные типы пространств, она идет гораздо дальше и позволяет строить схемы и новых пространств, еще не изученных. До сих пор математики мало обращали на них внимания, т.к. ни в самой Геометрии, ни в других науках в них не встречалось надобности. Но принцип относительности, его геометрическая интерпретация, предложенная Г. Минковским, заставляет нас создать, пользуясь теорией мероопределения, новые пространства, которые до сих пор еще не изучались, но которые должны теперь обратить на себя внимание геометров. §5. Обращаясь к построению мира Г. Минковского и мира Ньютона, мы всегда в дальнейшем будем предполагать, что все наши построения происходят в пространстве проективном, в котором имеют место аксиомы проективной Геометрии. ... §11. Вообразим четырехмерное проективное пространство R4 и возьмем в нем линейное трехмерное пространство Р3, которое назовем бесконечно удаленным. С этим пространством Р3 всякая прямая пересечется в одной точке, плоскость – по прямой линии, и линейное трехмерное пространство – по плоскости. ... §12. Возьмем наконец за абсолют Р3 пространство Лобачевского трех измерений и пусть его абсолютом служит некоторая поверхность S2 второго порядка. Каждая прямая пространства R4 встретит пространство Л3 = P3 только в одной точке, в конце прямой, каждая плоскость пересечется с Л3 по бесконечно удаленной прямой и каждое линейное пространство трех измерений – по бесконечно удаленной плоскости. Концы двух взаимно перпендикулярных линий пространства R4 сопряжены по отношению к поверхности S2, а линии пересечения с Л3 двух перпендикулярных плоскостей образуют взаимные поляры S2. Концы осей ортогональной системы Oxyzt находятся в вершинах автополярного по отношению к S2 тетраэдра. Замена одной координатной системы другой соответствует замене одного тетраэдра x, y, z, t другим x′, y′, z′, t′. Если t, конец оси t, находится внутри поверхности S2, есть точка реальная, то точки x, y, z, концы осей х, у, z, будут идеальными. Плоскости yzt, zxt, xyt пересекутся с поверхностью S2 по действительным кривым и будут плоскостями Лобачевского, координатные же пространства Oyzt, Ozxt, Oxyt пространствами Минковского трех измерений. Плоскость xyz будет плоскостью Римана, а пространство Oxyz – обыкновенным пространством Евклида. Этот характер координатных пространств убеждает нас в том, что геометрические свойства фигур четырехмерного пространства Oxyzt, устанавливая связь между х, у, z, t и их производными, будут выражать законы механики Einstein'а. Пространство R4 ≡ M4 ≡ (Л3E) будет, следовательно, миром Минковского четырех измерений, и преобразование Лоренца представится как переход от одного координатного тетраэдра xyzt, к другому x′y′z′t′. Движение точки m в Евклидовом пространстве Oxyz, заданное ур. x = f(t), y = f1(t), z = f2(t), представится в пространстве М4 мировой линией, касательная проведенная к ней в какой-нибудь точке M(x,y,z,t) пересечет абсолют Л3 в точке A0. Скорость точки m в момент t в системе (х, y, z, t) представится вектором tA0 и будет равна v = c·sh u, (21) где u есть длина отрезка tA0. Рассуждая совершенно так же, как и в случае движения точки по прямой или по плоскости, мы можем установить однозначное соответствие между скоростями и точками абсолюта, остающееся неизменным при переходе от одной системы отсчета к другой. При этом скоростям, меньшим скорости света с, будут соответствовать реальные точки абсолюта Л3, лежащие внутри поверхности S2, скоростям большим чем с – точки идеальные, и, наконец, скоростям равным скорости света – точки самой поверхности S2. Мы можем поверхность S2 назвать световой поверхностью или световым абсолютом пространства Лобачевского Л3. Сложение скоростей приведется к сложению отрезков в пространстве Л3 и выразится основной тригонометрической формулой Геометрии Лобачевского, которая легко преобразуется в формулу Einstein'а. ... Я не буду более рассматривать примеров из кинематики динамики и обращу только внимание на то простое геометрическое толкование, которое получает электромагнитный вектор, т.е. вектор, состоящий из электрического смещения и магнитной силы, и закон, управляющий этим вектором при переходе от одной системы отсчета к другой. В своем мемуаре «Пространство и время» Г. Минковский говорит: «При описании поля, вызываемого электроном, оказывается, что разделение поля на электрическую и магнитную силы есть разделение относительное и зависит от избранной оси времен; наиболее целесообразно рассматривать одновременно обе силы, руководствуясь при этом известною, хотя и неполною, аналогией, силовым винтом механики». Эти слова Минковского должны быть исправлены в том смысле, что электромагнитный вектор представляет собой совершенно полную аналогию с винтом механики, но только не в пространстве Евклида, а в пространстве Лобачевского Л3, которое служит абсолютом миру Минковского. Действительно, рассмотрим кинематический винт пространства Лобачевского. Перемещение твердого тела в пространстве Лобачевского мы можем разложить на поступательное, которое определяется перемещением какой-нибудь точки А тела и задается вектором V, и вращательное, вокруг оси, проходящей через ту же точку А, и определяемое вектором Ω. Но это разложение перемещения на поступательное и вращательное относительно. Если бы для характеристики того же самого перемещения тела мы избрали бы другую точку В, то оно – перемещение – определилось бы двумя другими векторами V′ и Ω′, связанными с векторами V, Ω законами кинематики пространства Лобачевского. Эта зависимость между V, Ω и V′, Ω′ и будет как раз той зависимостью, которая связывает элементы одного и того же вектора, отнесенного один раз к системе отсчета (x, y, z, t), у которой концом оси t служит точка А, а в другой раз к системе (x′, y′, z′, t′), у которой конец оси t′ совпадает с точкой В. Едва ли проще можно представить себе эту зависимость. Она показывает нам, что каждому электромагнитному вектору соответствует винт в абсолюте Л3. Я не буду входить в дальнейшие подробности, ограничусь только общим замечанием, что теория векторов неевклидовых пространств, изложенная в моей работе: «Проективная теория векторов» (1899), имеет много общего с теорией векторов мира Минковского, разработанной A. Sommerfeld′ом в его мемуаре: «Zur Relativitätstheorie». Та точка зрения, которую устанавливает на мир Минковского проективная Геометрия, как на пространство четырех измерений, абсолютом которому служит трехмерное пространство Лобачевского, представляет теорию векторов мира Минковского в новом освещении, благодаря которому эта теория значительно выигрывает в простоте и ясности и связывается самым тесным образом с теорией векторов в пространстве Лобачевского. Вместе с тем устанавливается связь между геометрической интерпретацией принципа относительности при помощи Геометрии Лобачевского, предложенной Varičak'ом, и миром Минковского, и становится ясным, что реальная часть пространства Лобачевского Л3, которая служит абсолютом мира Минковского, и есть то пространство, которым пользуется Varičak в своих многочисленных работах. Итак, резюмируя всё выше сказанное, мы видим, что механика Евклидова пространства трех измерений может быть рассматриваема как Геометрия мира (х, у, z, t) четырех измерений. Для классической механики мы имеем мир Ньютона N4, для механики Einstein'а – мир Минковского М4. Бесконечно удаленные элементы мира образуют его абсолют. Абсолютом мира Ньютона служит обыкновенное трехмерное Евклидово пространство; абсолютом последнего – мнимое коническое сечение (шаровой круг). Абсолютом мира Минковского служит трехмерное пространство Лобачевского; абсолютом последнего – световая поверхность 2-го порядка. Так как Геометрией Лобачевского определяются метрические свойства мира Минковского, а эти свойства выражают законы принципа относительности, то можно сказать, что Геометрия пространства Лобачевского трех измерений определяет законы механики Einstein'а. В том же смысле Геометрия Евклидова пространства трех измерений определяет законы механики Ньютона. А.П. Котельников. Принцип относительности и Геометрия Лобачевского, In mem. Lobatschevskii, 1927, том 2, 37–66 https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=kumem&paperid=6&option_lang=rus |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5179
Зарегистрирован: 27.08.07
|
|

Отправлено: 14.03.23 16:57. Заголовок: Некоторые применения..
Некоторые применения идей Лобачевского в механике и физике    Геометрические знания составили основу всей точной науки, а самобытность геометрии Лобачевского — зарю самостоятельного развития наук в России. Посев научный взойдет для жатвы народной. Д.И. Менделеев.  От редакции Настоящий второй выпуск серии «Геометрия Лобачевского и развитие ее идей» содержит две статьи, посвященные применению неевклидовой геометрии в механике и физике. Обе статьи были написаны еще до второй мировой войны (они должны были, по первоначальному замыслу, сопровождать сочинения Лобачевского); несмотря на это, они сохранили интерес и актуальность до сих пор. Первая статья ныне покойного профессора А.П. Котельникова содержит изложение основ механики неевклидова пространства. Математический аппарат, при помощи которого строятся основы механики евклидова пространства, опирается на теорию векторов; для установления тех же начал механики в неевклидовом пространстве потребовалась специальная векторная алгебра, которая и была разработана А.П. Котельниковым в его труде «Проективная теория векторов» в 1899 году. Чрезвычайно интересно, что ход развития этой теории привел к идеям, оказавшимся плодотворными для геометрии не только неевклидова, но и евклидова пространства. Эти идеи отчетливо выяснены в статье А.П. Котельникова. Вторая статья, принадлежащая академику В. А. Фоку, очень интересна в том отношении, что она выявляет, как разнообразны вопросы современной физики, в которых находит применения геометрия Лобачевского; более того, в этой статье освещаются те стороны физической реальности, для которых геометрия Евклида является недостаточной.  А.П. Котельников Теория векторов и комплексные числа (начала механики в неевклидовом пространстве) Первые работы Де-Тилли и А. Дженноки, относящиеся к механике в пространстве Лобачевского, были вызваны желанием исследовать вопрос, не находится ли геометрия Лобачевского в противоречии с принципами механики. Хотя с первых же шагов в этих исследованиях мы встречаем ряд парадоксальных теорем, однако эти парадоксы такого же характера, как и те, с которыми нам приходится иметь дело в неевклидовой геометрии, как, например, теорема о невозможности в пространстве Лобачевского построить треугольник, площадь которого превосходила бы сколько угодно большую наперед заданную величину. В них нет логического противоречия, и, таким образом, изучение движения и равновесия тел в неевклидовых пространствах приводит нас к тому убеждению, что принципы механики совместны с неевклидовой геометрией и что мы с полным правом можем говорить о механике в неевклидовых пространствах. Вместе с тем уже первые попытки изучить статику и кинематику твердого тела в пространстве Лобачевского, сделанные Де-Тилли, Дженноки, Линдеманом, Андрадом и др., привели к тому результату, что аналогия между статикой и кинематикой твердого тела, обнаруженная для евклидова пространства Пуансо в его классическом мемуаре «Theorie nouvelle de la rotation des corps» должна существовать и в механике неевклидовых пространств. Поэтому вполне естественно, что математическая обработка этих двух отраслей механики потребовала нового построения теории векторов. Исторический ход развития этой теории привел к двум новым идеям, оказавшимся плодотворными для геометрии не только неевклидова, но и евклидова пространства. До конца XIX столетия в теории векторов, т.е. в тех геометрических теориях, в которых нам приходится иметь дело с величинами, связанными с направлением или положением прямой линии, вектор всегда изображался прямолинейным отрезком или, иначе говоря, совокупностью двух точек: начала и конца вектора. Но принцип двойственности распространяется для неевклидовых пространств не только на проективные, но и на метрические свойства; это внушает мысль о необходимости наряду с фигурой, образованной двумя точками, рассматривать как элемент теории векторов фигуру, образованную двумя плоскостями (точкой и плоскостью), а затем и фигуру, образованную двумя прямыми линиями. Такова первая новая идея, возникшая на почве неевклидовой геометрии. Другая важная идея заключается в том, чтобы ввести в теорию комплексные числа с двумя единицами и некоторые их элементарные функции. Эти числа дают возможность установить соответствие между простыми геометрическими фигурами и более сложными и пользоваться первыми для изучения свойств последних. Введение чисел с двумя единицами приводит, таким образом, к особого рода приему, позволяющему переносить свойства одних фигур на другие, к особого рода принципу перенесения... А.П. Котельников, В.А. Фок. Некоторые применения идей Лобачевского в механике и физике. М.; Л.: ГИТТЛ, 1950. 88с. https://vk.com/s/v1/doc/dN_grMZa9VIJhWoy7IiwkR9RvBkLN6vlbIxQpnjQYMHnOS4J96w djvu Проективная теория векторов А.П. Котельникова, Казань, Издательство: Типо-литография Императорского Университета, 1899, 357с. Автор настоящей книги - известный российский математик А.П.Котельников - ввел понятие векторов особого рода, так называемых ""винтов"", тесно связанных с комплексными числами. В данной книге разработан математический аппарат винтового исчисления, аналогичный векторному, и векторный счет в проективном пространстве https://www.directmedia.ru/book-110308-proektivnaya-teoriya-vektorov/ Проблема сложения векторов в пространствах постоянной кривизны явилась одним из отправных пунктов творчества А.П. Котельникова. Во введении к докторской диссертации он, характеризуя наиболее существенные пункты, отличающие ее от работ других авторов, указывал, во-первых, что рассматривает кинематику и динамику твердого тела не по отдельности, но соединяет их в одну более отвлеченную теорию векторов, и, во-вторых, что «все указанные мною авторы задавали силу и скорость совокупностью прямой и числа, и только де Тилли и П. Юшкевич изобразили силы и скорость им пропорциональными отрезками прямой. Такое геометрическое представление у названных авторов, однако, не играет никакой существенной роли, и даже простейшим законом сложения сил и скоростей эти авторы, подобно всем другим, пользовались в его аналитической форме. Никто, насколько мне известно, не задавался вопросом, не следует ли, изображая силы и скорости прямолинейным отрезком, принять какую-нибудь другую зависимость между длиной этих отрезков и величиной изображаемых ими сил и скоростей вместо прямой пропорциональности, никто не задавался вопросом, нельзя ли основной закон механики — закон сложения сил и скоростей выразить в столь же простой геометрической форме, как и правило параллелограмма в евклидовом пространстве и, таким образом, придать механике твердого тела в неевклидовых пространствах более геометрический характер. Эти вопросы следует считать исходными вопросами моей работы. Они повели меня в свою очередь к более глубокому анализу тех предположений, которые необходимы с точки зрения проективной геометрии для формального обоснования теории векторов» (А.П. Котельников. Проективная теория векторов. Введение к докторской диссертации (отд. оттиск). Казань, 1899, с.29). Юшкевич А.П. История математики в России до 1917 года. - М.: Наука, 1968. - 592с.) http://pyrkov-professor.ru/default.aspx?tabid=186&ArticleId=631 |  |

|
|
|
|
Ять
|

| постоянный участник


|
Пост N: 5180
Зарегистрирован: 27.08.07
|
|

Отправлено: 15.03.23 18:38. Заголовок: Первый том Полного с..
Первый том Полного собрания сочинений Н.И. Лобачевского Новая Геометрия, основание которой уже здесь положено, если и не существует в природе, тем не менее может существовать в нашем воображении, и, оставаясь без употребления для измерений на самом деле, открывает новое, обширное поле для взаимных применений Геометрии и Аналитики – Н.И. Лобачевский. О началах геометрии  Т. 1. Сочинения по геометрии. Геометрические исследования по теории параллельных линий. О началах геометрии. Т. 2. Сочинения по геометрии. Геометрия. Новые начала геометрии с полной теорией параллельных. Т. 3. Сочинения по геометрии. Воображаемая геометрия. Применение воображаемой геометрии к некоторым интегралам. Пангеометрия. Т. 4. Сочинения по алгебре. Алгебра или вычисление конечных. - Понижение степени в двучленном уравнении, когда показатель без единицы делится на 8. Т. 5. Сочинения по математическому анализу, теории вероятностей, механике и астрономии. *** Рецензия Н.И. Лобачевский. Полное собрание сочинений под общей редакцией В.Ф. Кагана, А.П. Котельникова, В.В. Степанова, Н.Г. Чеботарёва, П.А. Широкова. Главный редактор В.Ф. Каган. Том первый— Сочинение по геометрии. Геометрические исследования по теории параллельных линий. О началах геометрии. Гостехиздат, 1946, М.—Л., 415с. Государственным технико-теоретическим издательством выпущен в свет первый том Полного собрания сочинений Н.И. Лобачевского (которое в целом рассчитано на 6 томов). Книга содержит два сочинения Н.И. Лобачевского: 1. «Геометрически исследования по теории параллельных линий» (1840) - в переводе В.Ф. Кагана, и 2. «О началах геометрии» (1824). Первое из них сопровождается вводными статьями и комментариями В.Ф. Кагана, второе — вводной статьёй и комментариями А.П. Котельникова. Начиная полное собрание сочинений Лобачевского с «Геометрических исследований...» и отступая тем самым от хронологической последовательности его работ, редакция издания руководствовалась тем, что сочинение «Геометрические исследования...» по характеру изложения является наиболее доступным среди всех геометрических сочинений Лобачевского. Здесь Лобачевский излагает элементарную часть своего учения: неевклидову теорию параллельных линий, геометрию на предельной поверхности, вывод выражения функци П (х). В настоящем издании изложение Лобачевского поясняется многочисленными примечаниями, помещёнными отчасти в сносках, а главным образом — в конце его текста. Первая вводная статья В.Ф. Кагана «Учение о параллельных линиях и открытие неевклидовой геометрии» содержит много интересных отрывков из сочинений -Прокла, Евклида, Нассир-Эддина, Валлиса, Л. Бертрана, Лежандра и выдержки и переписки Гаусса; особенно интересным нам представляется цитированные на стр. 35 комментарий Прокла. Конец статьи посвящен краткой биографии Лобачевского. Вторая вводная статья В.Ф. Кагана посвящена обзору сочинения «Геометрические исследования...». Помещённая во второй части тома работа Лобачевского «О началах геометрии» является его первым опубликованным (1829г.) исследованием. В нем даётся чрезвычайно сжатое в наиболее ответственных местах и трудно для чтения изложение неевклидовой геометрии, доведённой до формул для элементов дуги, площади и объёма в некоторых специальных координатах. В этой работе обращают на себя внимание следующие обстоятельства. 1. Попытка Лобачевского определить основные понятия геометрии, отправляясь от понятия расстояния. Хотя, как известно, задача обоснования геометрии решена Гильбертом в другой постановке, но и такая ее постановка является вполне законной. В современных терминах это есть задача об условиях, при которых метрическое пространство — евклидово (или, вообще, — пространство постоянной кривизны). 2. Попытка Лобачевского выяснить геометрические свойства физического пространства и тем самым установить, какая из двух известных ему геометрий является «употребительной» в звёздных масштабах (здесь проявляются отчётливо материалистические взгляды Лобачевского, с точки зрения которого вопрос о приложимости геометрии может решить только опыт). 3. Идея о приложимости неевклидовой геометрии к вычислениям математического анализа. На этом пути Лобачевский искал подтверждения логической непротиворечивости своей теории (для знакомства с вычислениями определённых интегралов, которые предпринимал Лобачевский, необходимо обращаться к его подлинным работам, так как в учебной литературе этот материал не содержится). Вводная статья А.П. Котельникова посвящена обзору сочинения «О началах геометрии». В конце текста Лобачевского даны многочисленные примечания (А.П. Котельникова) и приложения историко-библиографического характера. В примечаниях содержатся интересные для преподавателей решения неевклидовых задач на построения (стр. 265 и далее) - В заключение отметим прекрасное, выдержанное в строгих тонах, внешнее оформление книги. Н.В. Ефимов. Н.И. Лобачевский, “Полное собрание сочинений”, том I (рецензия), УМН, 1947, том 2, выпуск 6, 251 https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=rm&paperid=7006&option_lang=rus   А.П. Котельников. Обзор сочинения «О началах геометрии» В работе «О началах геометрии» Лобачевским намечены все те темы, которым были посвящены все последующие его геометрические работы; в дальнейших сочинениях эти темы нашли более полное развитие, а иногда и более простое изложение. Сочинение «О началах геометрии» можно разделить на три части. В первой части, представляющей собой извлечение из «Exposition succinеte», устанавливаются основные геометрические понятия, излагаются свойства треугольников, теория параллельных и выводятся тригонометрические формулы. Весь этот обширный материал изложен очень кратко, в подавляющем большинстве случаев почти без всяких доказательств, и первая часть имеет характер краткого конспекта. «Изложение всех моих исследований в надлежащей связи потребовало бы слишком много места и представления в совершенно новом виде вcей науки»,— пишет Лобачевский. И действительно, план, набросанный в первой части, совершенно не соответствует тому порядку, которому следуют обычно при изложении начал геометрии. Сначала вводится понятие о геометрическом теле, поверхности, линии и точке, причем за исходное единственное геометрическое свойство тела принимается прикосновение. Далее вводится расстояние между двумя точками, понятия о сфере и окружности предшествуют понятиям о плоскости и прямой линии. Одновременно рассматриваются углы линейные, плоскостные (двугранные) и телесные, и определяются все виды правильных многогранников. Установив основные понятия, Лобачевский перечисляет свойства прямолинейных и сферических треугольников и далее пишет: «...сумма углов прямолинейного треугольника не может быть > Pi. Остается предполагать эту сумму = Pi или < Pi. То и другое может быть принято без всякого противоречия в последствии, от чего и происходят две Геометрии — одна, употребительная до ныне по своей простоте, соглашается со всеми измерениями на самом деле; другая, воображаемая, более общая...». После этого перечисляются основные свойства параллельных в воображаемой геометрии, вводится угол параллельности и понятие о предельной линии и поверхности, в которые обращаются окружность и сфера, когда их центр удаляется в бесконечность. «Геометрия на предельной сфере совершенно та же, в каком виде мы ее знаем на плоскости»), — утверждает Лобачевский без всякого доказательства. Пользуясь этим свойством предельной поверхности, Лобачевский, при помощи соотношений между углами прямоугольного треугольника и углами параллельности, соответствующими его сторонам (формулы (3), (4), (5)), выводит основную формулу с «воображаемой геометрии» tang ½*F(a)= e^(-a) определяющую связь между длиной отрезка и отвечающий ему углом параллельности. Эта последняя вместе с предыдущими формулами дает возможность получить тригонометрические соотношения для прямоугольного, а затем и косоугольного прямоугольного треугольника. Выводом тригонометрических формул и заканчивается первая часть, — извлечение из «Exposition succinеte des principles de la Geometria etc». Лобачевского, конечно, очень интересовал вопрос, насколько его «воображаемая геометрия» отражает геометрические соотношения нашего физического пространства, и, переходя ко второй части своей работы он показывает, пользуясь паралаксами неподвижных звезд, что «...все линии, которые подлежат нашему измерению, даже расстояния между небесными телами, столько малы в сравнении с линиею, принятою в теории за единицу, что употребительные до сих пор уравнения прямолинейной Тригонометрии, без чувствительной погрешности должны быть справедливы...».   «…Как бы то ни было - заканчивает Лобачевский свое натур-философское отступление, — новая Геометрия, основание которой уже здесь положено, если и не существует в природе, тем не менее может существовать в нашем воображении, и, оставаясь без употребления для измерений на самом деле, открывает новое, обширное поле для взаимных применений Геометрии и Аналитики». Н.И. Лобачевский. “Полное собрание сочинений”, том I. 1946 https://www.klex.ru/161v https://vk.com/s/v1/doc/BzeoKoYeh-mx3e2tgIdepqENjbyHlYDEO_Y4vfGP7n3k5mMx_as Н.И. Лобачевский. Полное собрание сочинений по геометрии. Том 1. Казань, 1883. 561с. http://books.e-heritage.ru/book/10070447 |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5185
Зарегистрирован: 27.08.07
|
|

Отправлено: 17.03.23 06:34. Заголовок: К Евангелине Лобачев..
К Евангелине  Лобачевский. Речь о важнейших предметах воспитания 
Вот уже год прошел, любезные мои товарищи, как по избранию вашему, несу я на себе должность, которой почести, важность и трудности служат доказательствами лестной вашей ко мне доверенности. Не смею жаловаться на то, что вы захотели отозвать меня от любимых мною занятий, которым долгое время предавался я по склонности. Вы наложили на меня новые труды и чуждые до того мне заботы; но я не смею роптать, потому что вы предоставили мне и новые средства быть полезным. Я принял ваш вызов, потому что уважал вашим мнением; потому что не хотел противиться общему желанию; потому что сам первый не мог оправдать того, кто на моем месте вздумал бы отказаться. Наконец, выбор ваш утвержден был государем императором, и обязанности нового звания сделались для меня священными <...>.
Я сравниваю теперь себя с кормчим, который, не доверяя опытности, держался берегов; наконец решается плыть в открытое море, и не робкое путешествие свое рассказывать, но советов просить должен. В воспитании юношества, в сем важном деле, где я по званию своему участвую более других членов Университета, в исполнении сей важной обязанности прошу ваших советов. Осмеливаюсь подвергнуть вашему суждению мои мысли, полагая, что они заключают в себе первые основания нравственности и могут указывать на те правила, которым следовать обязаны наставники. Ими намерен и я руководствоваться, как путешественник, чтобы не сбиться с пути, смотрит на приметы, расставленные по дороге.
[II]
В каком состоянии, воображаю, должен бы находиться человек, отчужденный от общества людей, отданный на волю одной дикой природе! Обращаю потом мысли к человеку, который, среди устроенного, образованного гражданства последних веков просвещения, высокими познаниями своими составляет честь и славу своего отечества. Какая разность, какое безмерное расстояние разделяет того и другого. Эту разность произвело – воспитание. Оно начинается от колыбели, приобретается сперва одним подражанием, постепенно развертывается ум, память, воображение, вкус к изящному, пробуждается любовь к себе, к ближнему, любовь славы, чувство чести, желание наслаждаться жизнию. Все способности ума все дарования, все страсти, все это обделывает воспитание, соглашает в одно стройное целое, и человек, как бы снова родившись, является творение в совершенстве.
Наружный вид его, возвышенное чело, взор, который всюду устремляется, все созерцает вверху, вокруг себя; черты лица, в которых изображается чувственность, покоренная уму, – все показывает, что он родился быть господином, повелителем, царем природы. Но мудрость, с которой он должен править с наследственного своего престола, не дана ему от рождения: она приобретается учением.
В чем же должна заключаться эта мудрость? Чему должно нам учиться, чтобы достигнуть своего назначения? Какие способности должны быть раскрыты и усовершенствованы, какие должны потерпеть перемены; что надобно придать, что отсечь, как излишнее, вредное?
Мое мнение: ничего не уничтожать и все усовершенствовать. Неужели дары природы напрасны? Как осмелимся оcуждать их? Кого обвиним в них? Одного признаем виновника всему, что ни существует; исповедуем его и благоговеем пред его бесконечною премудростию <...>.
Что же надобно сказать о дарованиях умственных, врожденных побуждениях, свойственных человеку желаниях? Все должно остаться при нем: иначе исказим его природу, будем ее насиловать и повредим его благополучию.
Обратимся, во-первых, к главнейшей способности, уму, которым хотят отличить человека от прочих животных, противуполагая в последних инстинкт. Я не того мнения, чтобы человек лишен был инстинкта, который является во многих действиях ума, который в соединении с умом составляет Гений. Замечу только мимоходом, что инстинкт не приобретается; Гением быть нельзя, кто не родился. В этом-то искусство воспитателей: открыть Гений, обогатить его познаниями и дать свободу следовать его внушениям. Ум, если хотят составить его из воображения и памяти, едва ли отличает нас от животных? Но разум, без сомнения, принадлежит исключительно человеку; разум – это значит известные начала суждения, в которых как бы отпечатались первые действующие причины вселенной и которые соглашают, таким образом, все наши заключения с явлениями в природе, где противоречия существовать не могут.
[III]
Как бы то ни было, но в том надобно признаться, что не столько уму нашему, сколько дару слова одолжены мы всем нашим превосходством пред прочими животными. Из них самые близкие по сложению своего тела, как уверяют анатомики, лишены органов, помощию которых могли бы произносить сложные звуки. Им запрещено передавать друг другу понятия. Одному человеку предоставлено это право; он один на земле пользуется сим даром; ему одному велено учиться, изощрять свой ум, искать истин соединенными силами. Слова, как бы лучи ума его, передают и распространяют свет учения. Язык народа – свидетельство его образованности, верное доказательство степени его просвещения.
Чему, спрашиваю я, одолжены своими блистательными успехами в последнее время математические и физические науки, слава нынешних веков, торжество ума человеческого? Без сомнения, искусственному языку своему, ибо как назвать все сии знаки различных исчислений, как не особенным, весьма сжатым языком, который, не утомляя напрасно нашего внимания, одной чертой выражает обширные понятия. Такие успехи математических наук, затмивши всякое другое учение, справедливо удивляют нас; заставляют признаться, что уму человеческому предоставлено исключительно познавать сего рода истины, что он, может быть, напрасно гоняется за другими; надобно согласиться и с тем, что математики открыли прямые средства к приобретению познаний. Еще не с давнего времени пользуемся мы сими средствами. Их указал нам знаменитый Бакон. Оставьте, говорил он, трудиться напрасно, стараясь извлечь из одного разума всю мудрость; спрашивайте природу, она хранит все истины и на вопросы ваши будет отвечать вам непременно и удовлетворительно. Наконец, Гений Декарта привел эту счастливую перемену, и, благодаря его дарованиям, мы живем уже в такие времена, когда едва тень древней схоластики бродит по университетам. Здесь, в это заведение вступивши, юношество не услышит пустых слов без всякой мысли, одних звуков без всякого значения. Здесь учат тому, что на самом деле существует, а не тому, что изобретено одним праздным умом. Здесь преподаются точные и естественные науки, с пособием языков и познаний исторических <...>.
Как жалко, что истинному просвещению предпочитаются суетные выгоды домашнего воспитания. Кто хочет образовать своих детей для государства, тот должен прибегнуть к средствам, которые одно только государство в состоянии доставить; тот должен учить своих детей в общественных заведениях.
[IV]
Одно образование умственное не довершает еще воспитание. Человек, обогащая свой ум познаниями, еще должен учиться уметь наслаждаться жизнию. Я хочу говорить об образованности вкуса.
Жить – значит чувствовать, наслаждаться жизнию, чувствовать непрестанно новое, которое бы напоминало, что мы живем. Так, стихотворец наш Державин говорит о людях:
Непостоянство – доля
смертных,
В переменах вкуса – счастье
их.
Среди утех своих несметных
Желаем мы утех иных.
Единообразное движение мертво. Покой приятен после трудов и скоро обращается в скуку. Наслаждение заключается в волнении чувств, под тем условием, чтобы оно держалось в известных пределах. Впрочем, все равно, на веселое или печальное обращается наше внимание. И возвраты к унынию приятны; и трогательные картины бедствий человеческих нас привлекают. С удовольствием слушаем мы Эдипа на сцене театра, когда он рассказывает о беспримерных своих несчастиях. Веселое и печальное, как две противные силы, волнуют жизнь нашу внутри той волны, где заключаются все удовольствия, свойственные человеческой природе. Или подобно реке она [жизнь] течет в излучистых берегах: то разливается в лугах радости, то обмывает крутые утесы горестных размышлений. Ничто так не стесняет сего потока, как невежество: мертвою, прямою дорогою провожает оно жизнь от колыбели к могиле. Еще в низкой доле изнурительные труды необходимости, мешаясь с отдохновением, услаждают жизнь земледельца и ремесленника; но вы, которых существование несправедливый случай обратил в тяжелый налог другим; вы, которых ум отупел и чувство заглохло; вы не наслаждаетесь жизнию. Для вас мертва природа, чужды красоты поэзии, лишена прелести и великолепия архитектура, незанимательна история веков. Я утешаюсь мыслию, что из нашего университета не выйдут подобные произведения растительной природы; даже не войдут сюда, если, к несчастию, уже родились с таким назначением. Не выйдут, повторяю, потому, что здесь продолжается любовь славы, чувство чести и внутреннего достоинства <...>.
[VI]
Срочное время поручено человеку хранить огонь жизни; хранить с тем, чтобы он передал его другим. Он живет, чтобы оставить по себе потомство. Любовь к жизни, сильное побуждение во всех тварях, ты исполняешь высокую цель природы. Я переступил чрез вершину моей жизни, при первом шаге чувствую уже тяжесть, которая увлекает меня по отлогости второй половины моего пути. Всегда был я внимателен к явлениям организма; теперь не могу наблюдать, не могу говорить о них равнодушно <...>.
Яблоко, тронутое червем, зреет ранее других и валится на землю. Так порок сокращает жизнь; так юноша созревает преждевременно, удовлетворяя ранним своим желаниям, и ложится в могилу, когда бы ему надобно было цвести. Мы все живем втрое, вчетверо менее, нежели сколько назначено природой. Примерами это доказано: некто Екклестон жил 143 года. Генрих Женкинс – 169 лет. Натуралисты, сравнивая время возрастания человека и животных, приходят к тому же заключению: мы должны бы, говорят они, жить около 200 лет. Но увы, напрасно жизненная сила собирает питательные соки; их сожигает огонь страстей, снедают заботы и губит невежество. Пылкость нашего воображения, наше знание, всегда готовые воспоминания будят страсти и призывают желания не должные. Наставник юношества пусть обратит сюда внимание и постарается предупредить безрассудность молодости, еще не знающей цены своему здоровью <...>.
Будем же дорожить жизнию, покуда она не теряет своего достоинства. Пусть примеры в истории, истинное понятие о чести, любовь к отечеству, пробужденная в юных летах, дадут заранее то благородное направление страстям и ту силу, которые дозволят нам торжествовать над ужасом смерти. С повязкою на глазах, как говорит Рошефуко, мы его не увидим.
[VII]
Быть готову всякий час принести эту великую жертву требует от нас премудрость творца, вложившего в человеческое сердце с любовию к себе и любовь к ближнему. Отсюда проистекают все начала нравственности предмет воспитания, к которому, как важнейшему, прихожу я к последнему и не хочу говорить о нем, как о науке. Дюало, Рошефуко, Книеге объясняли, каким образом себялюбие бывает скрытою пружиной всех поступков человека в обществе. Кто, спрашиваю, умел в полноте изложить, какие обязанности проистекают из любви к ближнему. Были люди, каковы Гоббес и Гельвеций, которые не хотели верить, чтобы человек рожден был для общества. По счастию, заблуждение их не опасно: подобные будут являться, может быть, по временам; но последователей себе не найдут. Как можно усумниться, чтобы творец вселенной, которого признаем за существо благое, только с последним усилием ума дозволил достигать познания, самого необходимого для благополучия человека. Еще можем обойтись без писанных законов, когда они начертаны в сердцах наших. Мы родимся с добродетелями, и совесть дана им в охранение. Примеры научают лучше, нежели толкования и книги.
[VIII]
Вы, воспитанники сего заведения, вы пользовались сими примерами. Уверен, что вы отсюда донесете любовь и добродетели и сохраните ее вместе с благодарностию к вашим наставникам. Вы узнаете, и опыт света еще более уверит вас, что одно чувство любви к ближнему, любви бескорыстной, беспристрастной, истинное желание добра вам налагало на нас попечение просветить вам ум познаниями, утвердить вас в правилах веры, приучить вас к трудолюбию, к порядку, к исполнению ваших обязанностей, сохранить невинность ваших нравов, сберечь и укрепить ваше здоровье, наставить вас в добродетелях, вдохнуть в вас желание славы, чувство благородства, справедливости и чести, этой строгой неприкосновенной честности, которая бы устояла против соблазнительных примеров злоупотребления, недосягаемых наказанием.
Еще вы не в состоянии дать истинной цены словам моим, и не вдруг опытность может вразумить вас. Теперь вступаете вы в свет; новизна и многоразличность впечатлений не дает места размышлениям. Но придет время, когда на блеске настоящего вдруг явится прошедшее с обворожительною прелестию своего туска, подобно нежной затуманенной резьбе на ярком золоте, подобно отраженным предметам в слабом зеркале вод; тогда лета воспитания, лета беззаботной юности всеми невинными удовольствиями предстанут в вашем воспоминании, как образ совершенного счастия, невозвратимо потерянного. Тогда вашего товарища учения встретите вы как родного; тогда в разговоре о вашей юности с благодарностию будете произносить имена ваших наставников, признаетесь, сколь много они желали вам добра; и с торжеством друг другу дадите обещание следовать примерам, от нас слышанным.
[IX]
Расставаясь с вами, что скажу вам, самого поучительного? Вы счастливее меня, родившись позже. Из истории народов видели вы, что всякое государство переходит возрасты младенчества, возмужалости и старости. То же будет и с нашим любезным отечеством. Хранимое судьбою, медленно возвышается оно в своем величии и достигает высоты, на которую еще не восходило ни одно племя человеческое на земле. Век Петра, Екатерины, Александра были знамениты; но счастливейшие дни России еще впереди. Мы видели зарю, предвестницу их, на востоке; за нею показалось солнце...Я все сказал этим.
Н.И. Лобачевский. Речь о важнейших предметах воспитания (речь Н.И. Лобачевского на торжественном собрании Казанского университета 5 июля 1828г., в 1-ую годовщину пребывания на посту ректора. Впервые напечатано: Казанский Вестник. Казань, 1832. Ч. XXXV. Кн. VIII. Август. Отд. «Сочинения и переводы». с.577-596) https://runivers.ru/philosophy/chronograph/439163/
Первая публикация осуществлена в малоизвестном "Вестнике" Казанского университета (1832). Популяризацией речи мы обязаны академикам А.Н. Колмогорову и особенно П.С. Александрову. В годы войны Академия наук СССР была эвакуирована в Казань, то есть в город, в котором прошла почти вся жизнь Н.И. К 150-летию Лобачевского в военном 1943-м вышла в свет известная брошюра А.Н. Колмогорова и П.С. Александрова "Николай Иванович Лобачевский"
(ОГИЗ-Гостехиздат). К 150-летию открытия геометрии Лобачевского была издана большая монография "Н.И. Лобачевский. Научно-педагогическое наследие. Руководство Казанским университетом. Фрагменты. Письма" (М.: Наука, 1976) под редакцией П.С. Александрова, содержащая полный и подробно прокомментированный текст речи, воспроизводимый в "НГ-науке" с некоторыми сокращениями. При издании 1976 года для удобства были введены девять рубрик, отмеченных латинскими цифрами I–IX.
Проблемам воспитания посвящено множество весьма пространных текстов. Пожалуй, главная особенность речи Лобачевского определяется математическим складом мышления автора. Как и в геометрии, он поставил перед собой дерзкую философскую проблему: "А каковы они – важнейшие предметы воспитания?" И предложил очень краткое ее решение – разумеется, решение не единственное, но чрезвычайно яркое и убедительное.
Хочу обратить внимание на заключительный абзац, проникнутый и ответственностью за судьбы Отечества, и глубокой верой в славное будущее России. Что это? Ошибка Лобачевского? Нет. Это большой укор нам, гражданам современной России.
https://www.ng.ru/nauka/2009-12-02/14_lobachevsky.html

«Для них и солнцы, знать, не дышат,
И жизни нет в морских волнах.
Лучи к ним в душу не сходили,
Весна в груди их не цвела,
При них леса не говорили
И ночь в звездах нема была».
Тютчев
«…но вы, которых существование несправедливый случай обратил в тяжелый налог другим; вы, которых ум отупел и чувство заглохло, вы не наслаждались жизнию! Для вас мертва природа, чужды красоты ПОЭЗИИ, лишена прелести и великолепия архитектура, незанимательна история веков. Я утишаюсь мыслию, что из нашего Университета не выйдут подобные произведения растительной природы; даже не войдут сюда, если, к несчастью, родились с таким назначением. Не выйдут, повторяю, потому, что здесь продолжается любовь славы, чувство чести и внутреннего достоинства».
Лобачевский
Приведенные слова Лобачевского взяты из его знаменитой речи «О важнейших предметах воспитания», произнесенной 5 июля 1828г. и являющейся программной для всей деятельности Лобачевского как воспитателя юношества. Несомненно, что именно воспитателем юношества в первую очередь чувствовал себя Лобачевский в многообразии своих ректорских обязанностей. Все остальные стороны его организационной деятельности составляли только рамку для двух основных устремлений его жизни: творческой научной деятельности и деятельности воспитательной. Эта последняя воспринималась им с исключительной широтой и охватывала все стороны формирующейся личности молодого человека, начиная с физического развития и кончая специальным научным образованием. Проблемы воспитания интересовали его во всем их объеме и самым горячим образом. Еще с 1818г. он состоял членом Училищного комитета, ведавшего средними и низшими школами, и с тех пор не терял из виду, наряду с вопросами университетского образования, и всех сторон собственно школьного преподавания.
В частности, постоянно председательствуя в комиссии по приемным экзаменам в университет, Лобачевский прекрасно знал, с какими знаниями школьник того времени приходил в высшее учебное заведение. Лобачевский интересовался и занимался всей линией развития человека — от детского до позднего юношеского возраста. Из приведенных выше слов его видно, как высоки были задачи, которые он ставил перед воспитанием, и как полнозвучен и содержателен был тот идеал человека, к достижению которого воспитательная деятельность, по его мнению, должна была стремиться.
Речь Лобачевского «О важнейших предметах воспитания» является действительно замечательным памятником не только педагогической мысли, но, если позволительно так выразиться, и той воспитательной эмоции, которая необходимо должна сопровождать педагогическую деятельность, если считать, что ее задачи заключаются не только в том, чтобы научить молодого человека тем или иным знаниям, но и выпустить его в жизнь с определенными жизненными устремлениями и устоями. Этой «воспитательной эмоцией», соединенной с продуманными отчетливо сформулированным общим мировоззрением, имевшим своим жизненным основанием и подлинные творческие озарения, с одной стороны, и огромную, дисциплинированную и прекрасно организованную ежедневную работу, — с другой, Лобачевский обладал, как, вероятно, никто из его современников, что и создавало неповторимый комплекс личных свойств, делавший из него педагога в самом высшем и волнующем смысле этого слова.
Сам Лобачевский обладал в полной мере разнообразием и широтой жизненных интересов, входивших в его идеал гармонически развитой человеческой личности. И он многого требовал от молодого человека, пришедшего в университет учиться: он прежде всего требовал от него, чтобы он был гражданином, который «высокими познаниями составляет честь и славу своего отечества», т.е. ставил перед ним в полном и высшем смысле слова патриотический идеал, основанный на высоком уровне данной специальной квалификации человека (студент пришел в университет, чтобы получить именно эту квалификацию специалиста в той или иной интеллигентной профессии). Далее им подчеркивается, что «одно образование умственное не довершает еще воспитания», и ставятся те большие требования к интеллигентному человеку как полноценному носителю интеллектуальной, этической и эстетической культуры, которые с такой яркостью высказаны Лобачевским в словах, выбранных нами в качестве эпиграфа.
...Жизнь Лобачевского была мало похожа на жизнь «кабинетного ученого». Вся она была наполнена большим внутренним волнением, большим драматизмом. Постоянное, бескорыстное и — в тех условиях непонятости и непризнания, в которых он находился,— прямо героическое искание отвлеченной научной истины, с одной стороны, и горячая любовь к родной стране, к ее просвещению, к ее молодежи, с другой,— вот те две основные пружины, которые сообщали жизни Лобачевского все ее необыкновенное эмоциональное движение, ее полет, ее патетику. Характеристикой всего внутреннего облика Лобачевского могут служить его же слова, сказанные им в уже упомянутой «Речи о важнейших предметах воспитания»: «Жить — значит чувствовать, наслаждаться жизнию, чувствовать непрестанно новое, которое бы напоминало, что мы живем...Будем же дорожить жизнию, пока она не теряет своего достоинства. Пусть примеры в Истории, истинное понятие о чести, любовь к отечеству, пробужденная в юных летах, дадут заранее то благородное направление страстям и ту силу, которые дозволят нам торжествовать над ужасом смерти».
П.С. Александров. Н.И. Лобачевский. Краткий очерк его жизни и деятельности (с.562-593)
Речь о важнейших предметах воспитания (речь Н.И. Лобачевского на торжественном собрании Казанского университета 5 июля 1828г., в 1-ую годовщину пребывания на посту ректора. Впервые напечатано: Казанский Вестник. Казань, 1832. Ч. XXXV. Кн. VIII. Август. Отд. «Сочинения и переводы». с.577-596)
Вот уже год прошел, любезные мои товарищи, как по избранию вашему, несу я на себе должность, которой почести, важность и трудности служат доказательством лестной вашей ко мне доверенности. Не смею жаловаться на то, что Вы захотели отозвать меня от любимых мною занятий, которым долгое время предавался я по склонности. Вы наложили на меня новые труды и чуждые до того мне заботы; но я не смею роптать, потому что вы предоставили мне новые средства быть полезным.
Я принял ваш вызов, потому что уважал вашим мнением; потому что не хотел противиться общему желанию; потому что сам первый не мог оправдать того, кто на моем месте вздумал бы отказаться...
Н.И. Лобачевский. Избранные труды по геометрии. М.: Изд-во АН СССР, 1956. c.421-430
https://vk.com/doc399489626_450217586
H.И. Лобачевский. О важнейших предметах воспитания
https://web.archive.org/web/20180201190943/http://sinsam.kirsoft.com.ru/KSNews_209.htm
Воображаемая геометрия
https://web.archive.org/web/20180201190943/http://sinsam.kirsoft.com.ru/KSNews_798.htm
|  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5187
Зарегистрирован: 27.08.07
|
|

Отправлено: 18.03.23 19:12. Заголовок: Речь И. И. Лобачевск..
Н.И. Лобачевский. Речь о важнейших предметах воспитания ...В начале речи Лобачевский, отметив, что он уже год трудится на посту ректора, вспоминает, как нелегко ему было оторваться от научных занятий. Он принял должность ректора, лишь подчиняясь мнению товарищей и стремясь принести пользу университету. Он жалуется на недостаточность своих сил, но его ободряет улучшение обстоятельств и внимание попечителя. Называя протекший год годом испытания, он надеется, что следующий будет годом исполнения, а третий - годом успеха (торжества моего) и просит критики и советов по поводу высказываемых им далее принципов воспитания. Затем он останавливается на роли воспитания и образования, преобразующих дикого человека в гармонично развитого просвещенного члена общества. Ничто не должно подавляться, даже страсти полезны в обществе, только их направление может быть вредно. Касаясь понятий инстинкта, ума и разума, Лобачевский характеризует гений как соединение инстинкта (здесь, повидимому, подразумевается то, что мы называем интуицией) с умом и ставит задачу перед воспитателями - открыть гениальность в юноше, обогатить его познаниями, а далее дать ему свободу в его творчестве. Замечательна характеристика разума, т.е. логического мышления, включающая положение о познаваемости мира: Разум, это значит, известные начала суждения, в которых как бы отпечатались первые действующие причины Вселенной и которые соглашают таким образом все наши заключения с явлениями в природе, где противоречия существовать не могут. Особо подчеркивается значение языка в развитии просвещения. Необычайные успехи математических наук поставлены в связь с созданием и использованием специальной символики, т.е. как бы языков различных исчислений. Как примечательное достижение научной мысли охарактеризован “прямой метод научного познания”. Его “указал нам знаменитый Бакон” (Ф. Бэкон). “Оставьте, говорил он, трудиться напрасно, стараясь извлечь из одного разума всю мудрость; спрашивайте природу, она хранит все истины и на вопросы ваши будет отвечать вам непременно и удовлетворительно” (эксперимент – критерий истины). Гений Декарта разрушил схоластическую науку и теперь “едва тень древней схоластики бродит по университету”. Далее обрисовано реальное направление университетского образования и преимущества общественного воспитания перед домашним. Задачи воспитания Лобачевский понимает очень широко. Он стремится воспитать всесторонне развитого, жизнелюбивого человека, которому доступно и понимание красоты. Он говорит, что овладение специальными знаниями (“образование умственное”) еще не завершает воспитания, так как человек “еще должен учиться уметь наслаждаться жизнию”. Поэтому юноше необходимо прививать широкую общую культуру и воспитывать эстетическое чувство (“образованность вкуса”). Только тогда он воспримет жизнь в ее движении, будет постоянно увлечен ее новизной, найдет прекрасное в этом движении, в колебаниях противоборствующих сил, в восприятии то веселого, то печального. Лобачевский сурово осуждал невежество: “Мертвою, прямою дорогою провожает оно жизнь от колыбели к могиле”. И если у крестьян или ремесленников чередование необходимого изнурительного труда и отдыха еще “услаждает жизнь”, то у невежд-крепостников жизнь полностью теряет свое достоинство. Лобачевский восклицает: “Но вы, которых существование несправедливый случай обратил в тяжелый налог другим; вы, которых ум отупел и чувство заглохло, вы не наслаждаетесь жизнию. Для вас мертва Природа, чужды красоты Поэзии, лишена прелести и великолепия Архитектура, незанимательна История Веков”. И его радует мысль, что “из Университета не выйдут подобные произведения растительной природы, и даже не войдут сюда”. По Лобачевскому, человеку свойствен дух соревнования, желание превосходить других. И стремление ума возвыситься и прославиться является движущей силой бесконечного совершенствования человечества. Касаясь вопросов жизни и смерти, Лобачевский говорит, что теперь, когда он “переступил через вершину...жизни”, он воспринимает с особой остротой все явления органической природы. Он вскрывает диалектику жизни и смерти, ярко и эмоционально описывая процесс: растение – зерно – растение. Привлекая образ яблока, подтачиваемого червем, он требует от воспитателей оградить юношество от пороков, которые подобно червю сокращают жизнь. Но как преодолеть ужас смерти, “этой бездны все поглощающей”, ибо сознание неизбежности смерти может отравить человеку его существование. Лобачевский видит выход в пробуждении с юных лет “любви к отечеству” и “истинного понятия о чести”, т.е. высоких идеалов, которые будут способствовать проявлению творческого начала и дадут силу “торжествовать над ужасом смерти”. Лобачевский касается и вопросов этики. Будучи вынужден своей должностью (ректор) и обстоятельствами (актовая речь) связать хотя бы внешне вопросы морали с положениями христианской религии, он упоминает “премудрость Творца”, проявившуюся в том, что человеку свойственна не только любовь к самому себе, но и любовь к ближнему. В чувстве любви к ближнему Лобачевский видит основу общественной природы человека, возможность его нравственного воспитания. Он упрекает философов, которые, выявив роль любви к себе в развитии общества, забыли о роли любви к ближнему (Дюкло, Ларошфуко, Гельвеций), причем некоторые из них (Гоббс, Гельвеций) даже отрицали, что “человек рожден для общества”. Нравственность, как полагает Лобачевский, лучше воспитывать не рассуждениями, а с помощью живых примеров. Обращаясь к студентам, Лобачевский говорит, что примеры бескорыстной любви к ближнему и желания добра они видели у своих наставников, обучавших их и прививавших им высокие и добрые чувства, и хотя сейчас воспитанники еще не в состоянии оценить эти слова из-за множества впечатлений и недостатка жизненного опыта, но и для них “придет время, когда на блеске настоящего вдруг явится прошедшее с обворожительной прелестью своего туска, подобно нежной, затуманенной резьбе на ярком золоте, ...” и тогда они вспомнят с благодарностью годы учения и своих наставников. Основная мысль заключения “Речи”: “...Вы счастливее меня, родившись позже ..., ибо счастливейшие дни России впереди”,– выражает подлинные надежды и чувства Лобачевского. Б.Л. Лаптев. Николай Иванович Лобачевский. К 150-летию геометрии Лобачевского. 1826-1976. - Казань: Изд-во Казанского университета, 1976. - 136с. http://pyrkov-professor.ru/default.aspx?tabid=190&ArticleId=987  Вот уже год прошел, любезные мои товарищи, как по избранию вашему, несу я на себе должность, которой почасти, важность и трудности служат доказательством лестной вашей ко мне доверенности. Не смею жаловаться на то, что Вы захотели отозвать меня от любимых мною занятий, которым долгое время предавался я по склонности. Вы наложили на меня новые труды и чуждые до того мне заботы; но я не смею роптать, потому что вы предоставили мне и новые средства быть полезным. Я принял ваш вызов, потому что уважал вашим мнением; потому что не хотел противиться общему желанию; потому что сам первый не мог оправдать того, кто на моем месте вздумал бы отказаться... Пусть справедливо могу жаловаться на слабость сил моих и способность; но могут ли недостатки извинить меня, когда ревность к службе должна вознаграждать их... Итак, все, чего бы желать надобно, наконец, дано. Спрашивается, мы все ли исполняли, что от нас требовалось? Вот как трудно мне успокоить мою совесть, когда я обращаюсь мыслями на первый год моего управления делами университета. Вот как трудно мне в этот первой срок давать отчет за себя, за весь университет; надеяться на одобрение моих товарищей; родителей, которых дети воспитываются в сем заведении; всех посетителей, которые пришли быть судьями в общем деле и могли бы справедливо быть строгими судьями. Испрашиваю снисхождения Вашего, пп. пп., если принужден умолчать о том, что не почитаю достойным Вашего внимания. Пусть этот протекший год дозволено мне будет называть годом испытания, желал бы следующий иметь право назвать годом исполнения, и последний в трехлетии — годом торжества моего. Я сравниваю теперь себя с кормчим, который, не доверяя опытности, держался берегов; наконец, решается плыть в открытое море, и не робкое путешествие свое рассказывать, но советов просить должен. В воспитании юношества, в сем важном деле, где я по званию своему участвую более других членов Университета, в исполнении сей важной обязанности прошу ваших советов. Осмеливаюсь подвергнуть вашему суждению мои мысли, полагая, что они заключают в себе первые основания нравственности и могут указывать на те правила, которым следовать обязаны наставники. Ими намерен и я руководствоваться, как путешественник, чтобы не сбиться с пути, смотрит на приметы, расставленные по дороге. В каком состоянии, воображаю, должен бы находиться человек, отчужденный от общества людей, отданный на волю одной дикой природе. Обращаю потом мысли к человеку, который среди устроенного, образованного гражданства последних веков просвещения высокими познаниями своими составляет честь и славу своего отечества. Какая разность; какое безмерное расстояние разделяет того и другого. Эту разность произвело воспитание. Оно начинается от колыбели, приобретается сперва одним подражанием, постепенно развертывается ум, память, воображение, вкус к изящному, пробуждается любовь к себе, к ближнему, любовь славы, чувство чести, желание наслаждаться жизнию. Все способности ума, все дарования, все страсти, все это обделывает воспитание, соглашает в одно стройное целое, и человек, как бы снова родившись, является творение в совершенстве. Наружный вид его, возвышенное чело, взор, который всюду устремляется, все созерцает вверху, вокруг себя; черты лица, в которых изображается чувственность, покоренная уму,— все показывает, что он родился быть господином, повелителем, царем природы. Но мудрость, с которой он должен править с наследственного своего трона, не дана ему от рождения: она приобретается учением. В чем же должна заключаться эта мудрость? Чему должно нам учиться, чтобы постигнуть своего назначения? Какие способности должны быть раскрыты и усовершенствованы, какие должны потерпеть перемены; что надобно придать, что отсечь, как излишнее, вредное? Мое мнение: ничего не уничтожать и все усовершенствовать. Неужели дары природы напрасны? Как осмелимся осуждать их?— Кого обвиним в них? Одного признаем виновника всему, что ни существует; исповедуем его и благоговеем пред его бесконечною премудростию. Всего обыкновеннее слышать жалобы на страсти, но как «справедливо сказал Мабли: чем страсти сильнее, тем они полезнее в обществе; направление их может быть только вредно. Что же надобно сказать о дарованиях умственных, врожденных побуждениях, свойственных человеку желаниях? Все должно остаться при нем; иначе исказим его природу, будем ее насиловать и повредим его благополучию. Обратимся, во-первых, к главнейшей способности, уму, которым хотят отличить человека от прочих животных, противуполагая в последних инстинкт. Я не того мнения, чтобы человек лишен был инстинкта, который является во многих действиях ума, который в соединении с умом составляет Гений. Замечу только мимоходом, что инстинкт не приобретается; Гением быть нельзя, кто не родился. В этом-то искусство воспитателей: открыть Гений, обогатить его познаниями и дать свободу следовать его внушениям. Ум, если хотят составить его из воображения и памяти, едва ли отличает нас от животных? Но разум, без сомнения, принадлежит исключительно человеку; разум, это значит, известные начала суждения, в которых как бы отпечатались первые действующие причины вселенной и которые соглашают, таким образом, все наши заключения с явлениями в природе, где противоречия существовать не могут. Как бы то ни было, но в том надобно признаться, что не столько уму нашему, сколько дару слова, одолжены мы всем нашим превосходством пред прочими животными. Из них самые близкие по сложению своего тела, как уверяют анатомики, лишены органов, помощию которых могли бы произносить сложные звуки. Им запрещено предавать друг другу понятия. Одному человеку предоставлено это право; он один на земле пользуется сим даром; ему одному велено учиться изощрять свой ум, искать истин соединенными силами. Слова, как бы лучи ума его, передают и распространяют свет учения. Язык народа — свидетельство его образованности, верное доказательство степени его просвещения. Чему, спрашиваю я, одолжены своими блистательными успехами в последнее время математические и физические науки, слава нынешних веков, торжество ума человеческого? Без сомнения, искусственному языку своему, ибо как назвать все сии знаки различных исчислений, как не особенным, весьма сжатым языком, который, не утомляя напрасно нашего внимания, одной чертой выражает обширные понятия. Такие успехи математических наук, затмивши всякое другое учение, справедливо удивляют нас; заставляют признаться, что уму человеческому предоставлено исключительно познавать сего рода истины, что он, может быть, напрасно гоняется за другими; надобно согласиться и с тем, что математики открыли прямые средства к приобретению познаний. Еще не с давнего времени пользуемся мы сими средствами. Их указал нам знаменитый Бакон. Оставьте, говорил он, трудиться напрасно, стараясь извлечь из одного разума всю мудрость; спрашивайте природу, она хранит все истины и на вопросы ваши будет отвечать вам непременно и удовлетворительно. Наконец, Гений Декарта привел эту счастливую перемену и, благодаря его дарованиям, мы живем уже в такие врмена, когда едва тень древней схоластики бродит по Университетам. Здесь, в это заведение вступивши, юношество не услышит пустых слов без всякой мысли, одних звуков без всякого значения. Здесь учат тому, что на самом деле существует; а не тому, что изобретено одним праздным умом. Здесь преподаются точные и естественные науки с пособием языков и познаний исторических. Здесь преподаватели разделяют между собою предметы, которыми всю жизнь свою занимаются, еще с молодых лет почувствовав в себе охоту и некоторые дарования. Как жалко, что истинному просвещению предпочитаются суетные выгоды домашнего воспитания. Кто хочет образовать своих детей для Государства, тот должен прибегнуть к средствам, которые одно только Государство в состоянии доставить, тот должен учить своих детей в общественных заведениях. Одно образование умственное не довершает еще воспитание. Человек, обогащая свой ум познаниями, еще должен учиться уметь наслаждаться жизнию. Я хочу говорить об образовании вкуса. Жить — значит чувствовать, наслаждаться жизнию, чувствовать непрестанно новое, которое бы напоминало, что мы живем. Так стихотворец наш Державин говорит о людях: Непостоянство — доля смертных, В пременах вкуса — счастье их. Среди утех своих несметных Желаем мы утех иных. Единообразное движение мертво. Покой приятен после трудов и скоро обращается в скуку. Наслаждение заключается в волнении чувств, под тем условием, чтобы оно держалось в известных пределах. Впрочем все равно, на веселое или печальное обращается наше внимание. И возвраты к унынию приятны; и трогательные картины бедствий человеческих нас привлекают. С удовольствием слушаем мы Эдипа на сцене театра, когда он рассказывает о беспримерных своих несчастиях. Веселое и печальное, как две противные силы, волнуют жизнь нашу внутри той волны, где заключаются все удовольствия, свойственные человеческой природе. Или подобно реке она течет в излучистых берегах: то разливается в лугах радости, то обмывает крутые утесы горестных размышлений. Ничто так не стесняет сего потока, как невежество: мертвою, прямою дорогою провождает оно жизнь от колыбели к могиле. Еще в низкой доле изнурительные труды необходимости, мешаясь с отдохновением, услаждают жизнь земледельца и ремесленника; но вы, которых существование несправедливый случай обратил в тяжелый налог другим; вы, которых ум отупел и чувство заглохло; вы не наслаждаетесь жизнию! Для вас мертва природа, чужды красоты поэзии, лишена прелести и великолепия архитектура, незанимательна история веков. Я утешаюсь мыслию, что из нашего Университета не выйдут подобные произведения растительной природы; даже не войдут сюда, если к несчастию уже родились с таким назначением. Не выйдут, повторяю, потому что здесь продолжается любовь славы, чувство чести и внутреннего достоинства. Кажется природа, одарив столь щедро человека при его рождении, еще не удовольствовалась. Вдохнула в каждого желание превосходить других, быть известным, быть предметом удивления, прославиться; и таким образом возложило на самого человека попечение о своем усовершенствовании. Ум в непрестанной деятельности силится стяжать почести, возвыситься,— и все человеческое племя идет от совершенства к совершенству и где остановится? Другие обязанности отзывают и охлаждают стремление к славе. Срочное время поручено человеку хранить огонь жизни; хранить с тем, чтобы он передал его другим. Он живет, чтобы оставить по себе потомство. Любовь к жизни, сильное побуждение во всех тварях, ты исполняешь высокую цель природы. Я переступил чрез вершину моей жизни, при первом шаге чувствую уже тяжесть, которая увлекает меня по отлогости второй половины моего пути. Всегда был я внимателен к явлениям организма; теперь не могу наблюдать, не могу говорить о них равнодушно. Покоится жизнь в зерне растения под охранительной пленою против враждебных стихий; но деятельность их, наконец, улучшает время и до того беззаботная вдруг пробуждается от сна. Тогда, с превосходством еще сил, строит она орудное жилище против непрестанного нападения. Скоро, почувствовав не равной бой, помышляет о побеге и скрывается в новом зерне. Вот краткое описание явления жизни в растении, животном и человеке. Чем удержать это стремление к побегу изменяющей жизни? Как рано пробуждается оно, и как верно рассчитано бывает время. Посмотрите на этот прививок: он уже цветет в первую весну. Органическая сила в нем предчувствует, что отчужденной черен от родного дерева, не долговечен, и что ей надобно спешить с плодами. Посмотрите на огородные овощи, когда холодные ночи грозят им скорым морозом: вдруг останавливают они рост свой, и зерна в них спеют. Яблоко,тронутое червем, зреет ранее других и валится на землю. Так порок сокращает жизнь; так юноша созревает преждевременно, удовлетворяя ранним своим желаниям, и ложится в могилу, когда бы ему надобно было цвести. Мы все живем втрое, вчетверо менее, нежели сколько назначено природой. Примерами это доказано: некто Екклестон жил 143 года, Генрих Женкинс 169 лет. Натуралисты, сравнивая время возрастания человека и животных, приходят к тому же заключению: мы должны бы, говорят они, жить около 200 лет. Но увы, напрасно жизненная сила собирает питательные соки; их сожигает огонь страстей, снедают заботы и губит невежество. Пылкость нашего воображения, наше знание, всегда готовые воспоминания будят страсти и призывают желания не должные. Наставник юношества пусть обратит сюда внимание и постарается предупредить безрассудность молодости, еще не знающей цены своему здоровью. О, как бы расточительны мы были с нашей жизнью, если бы мысль о смерти еще не стояла на страже. Где более света, там гуще тень: так все премудро соглашено в мире. Животное следует слепо своему побуждению. Человек знает наслаждения, ищет их с выбором,утончает их; но он не большим пользуется превосходством — он знает, чего бы лучше не знать, знает, что он должен умереть. Мысль мучительная, которая отравляет все наши удовольствия, подобно мечу Дионисия, на волосе повешенному над головою. Смерть, как бездна, которая все поглощает, которую ничем наполнить нельзя; как зло, которое ни в какой договор включить не можно, потому что оно ни с чем нейдет в сравнение. Но почему же смерть должна быть злом? Мы живем одно настоящее мгновение; прошедшее все равно, как бы ни существовало; с будущим — последует тоже. Когда смерть придет, тогда все равно — сколько мы ни прожили. Мы повинуемся гласу природы, не в силах будучи ему противиться; но собственно для нас какая выгода, жить более или менее? Будем же дорожить жизнию, покуда она не теряет своего достоинства. Пусть примеры в Истории, истинное понятие о чести, любовь к отечеству, пробужденная в юных летах, дадут заранее то благородное направление страстям и ту силу, которые дозволят нам торжествовать над ужасом смерти. С повязкою на глазах, как говорит Рошефуко, мы его не увидим. Быть готову всякой час принести эту великую жертву требует от нас премудрость творца, вложившего в человеческое сердце с любовию к себе и любовь к ближнему. Отсюда проистекают все начала нравственности, предмет воспитания, к которому, как важнейшему, прихожу я к последнему, и не хочу говорить о ним, как о науке. Дюкло, Рошефуко, Книгге объясняли, каким образом самолюбие бывает скрытою пружиной всех поступков человека в обществе. Кто, спрашиваю, умел в полноте изложить, какие обязанности проистекают из любви к ближнему. Были люди, каковы Гоббес и Гельвеций, которые не хотели верить, чтобы человек рожден был для общества. По счастию, заблуждение их не опасно: подобные будут являться может быть по временам; но последователей себе не найдут. Как можно усумниться, чтобы творец вселенной, которого признаем за существо благое, только с последним усилием ума дозволил достигать познания, самого необходимого для благополучия человека. Еще можем обойтись без писанных законов, когда они начертаны в сердцах наших. Мы родимся с добродетелями и совесть дана им в охранение. Примеры научают лучше, нежели толкования и книги. Вы, воспитанники сего заведения, вы пользовались сими примерами. Уверен, что вы отсюда понесете любовь и добродетели и сохраните ее вместе с благодарностию к вашим наставникам. Вы узнаете, и опыт света еще более уверит вас, что одно чувство любви к ближнему, любви бескорыстной, беспристрастной, истинное желание добра вам налагало на нас попечение просветить ваш ум познаниями, утвердить вас в правилах веры, приучить вас к трудолюбию, к порядку, к исполнению ваших обязанностей, сохранить невинность ваших нравов, сберечь и укрепить ваше здоровье, наставить вас в добродетелях, вдохнуть в вас желание славы, чувство благородства, справедливости и чести, этой строгой, неприкосновенной честности, которая бы устояла против соблазнительных примеров злоупотребления, не досягаемых наказанием. Еще вы не в состоянии дать истинной цены словам моим, и не вдруг опытность может вразумить вас. Теперь вступаете вы в свет, новизна и многоразличность впечатлений не дает места размышлениям. Но придет время, когда на блеске настоящего вдруг явится прошедшее с обворожительною прелестию своего туска, подобно нежной затуманенной резьбе на ярком золоте, подобно отраженным предметам в слабом зеркале вод, тогда лета воспитания, лета беззаботной юности со всеми невинными удовольствиями предстанут в вашем воспоминании, как образ совершенного счастия, невозвратимо потерянного. Тогда вашего товарища учения встретите вы как родного; тогда в разговоре о вашей юности с благодарностию будете произносить имена ваших наставников, признаетесь, сколь много они желали вам добра, и с торжеством друг другу дадите обещание следовать примерам, от нас слышанным. Расставаясь с вами, что скажу вам самого поучительного? Вы счастливее меня, родившись позже. Из истории народов видели вы, что всякое государство переходит возрасты младенчества, возмужалости и старости. Тоже будет и с нашим любезным отечеством. Хранимое судьбою медленно возвышается оно в своем величии и достигает высоты, на которую еще не восходило ни одно племя человеческое на земли. Век Петра, Екатерины, Александра были знамениты; но счастливейшие дни России еще впереди. Мы видели зарю, предвестницу их, на востоке; за нею показалось солнце... Я все сказал этим. Н.И. Лобачевский. Избранные труды по геометрии. М.: Изд-во АН СССР, 1956. c.421-430 https://vk.com/doc399489626_450217586 - |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5188
Зарегистрирован: 27.08.07
|
|

Отправлено: 19.03.23 07:20. Заголовок: Взгляды Лобачевского..
Взгляды Лобачевского на математический метод и его значение  Обратимся, во-первых, к главнейшей способности, уму, которым хотят отличить человека от прочих животных, противуполагая в последних инстинкт. Я не того мнения, чтобы человек лишен был инстинкта, который является во многих действиях ума, который в соединении с умом составляет Гений. Замечу только мимоходом, что инстинкт не приобретается; Гением быть нельзя, кто не родился. В этом-то искусство воспитателей: открыть Гений, обогатить его познаниями и дать свободу следовать его внушениям. Ум, если хотят составить его из воображения и памяти, едва ли отличает нас от животных? Но разум, без сомнения, принадлежит исключительно человеку; разум, это значит, известные начала суждения, в которых как бы отпечатались первые действующие причины вселенной и которые соглашают, таким образом, все наши заключения с явлениями в природе, где противоречия существовать не могут. - Н.И. Лобачевский. Речь о важнейших предметах воспитания (1828) Научные интересы Лобачевского в области физико-математических наук были весьма широки. Его научные исследования не исчерпываются работами по новой геометрии. В различные годы, кроме математических курсов, он вел также преподавание механики, физики и астрономии (см. с.52–57). Он был глубоко осведомлен в этих науках, внимательно следил за современной научной литературой, и ему принадлежит несколько статей в этой области: две статьи об акустическом резонансе (1823, 1828), Примечания к статье А. Купфера “О температуре почвы” (1829), “Исследование о движении твердого тела” (1834) [1, т. 5], “Отчет о наблюдении полного затмения Солнца” (1842) [1, т. 5], где он высказал ценные мысли о необходимости сочетать волновую и корпускулярную теории света, и “Разбор докторской диссертации А.Ф. Попова об уравнениях гидродинамики” (1845) [1, т. 5]. В дальнейшем мы коснемся содержания только математических его трудов. Помимо идей новой геометрии он стремится осуществить в своих геометрических работах оригинальный подход к самым первым основным геометрическим понятиям. Мы уже упоминали, что он критиковал Евклида за то, что тот принимал в качестве исходных такие абстрактные понятия, как точка, линия и поверхность. В соответствии со своими материалистическими воззрениями на природу Лобачевский полагал, что начальные понятия должны быть более близки с непосредственно воспринимаемым нами объектам, к материальным телам. Они должны быть “приобретенными” с помощью наших чувств, и, только опираясь на эти первые понятия, следует вводить более отвлеченные “произведенные” понятия, так сказать абстракции второй ступени. С помощью неопределимого исходного понятия «прикосновение» он вводит понятие геометрического тела (когда от материального тела сохранено только понятие «прикосновение»). Затем рассматривает разные типы разделений тела на части (или сечений), в том числе два важнейших: поступательное и обращательное (или накрест). Соответственно прикосновение получается поверхностное или линейное. В случае, когда имеются три главных сечения тела и оно при этом разделяется на 8 частей, две части на противоположных сторонах имеют точечное прикосновение. Если у двух тел, имеющих поверхностное прикосновение, не рассматривать части, не касающиеся в одном теле другого, то получим поверхность. Аналогично определяется линия и точка. Введя расстояние как относительное положение двух точек Лобачевский дает определение сферы, далее плоскости (с помощью двух семейств концентрических сфер), окружности и, наконец, прямой (с помощью двух семейств концентрических окружностей на плоскости). Аксиоматический метод еще не был тогда достаточно разработан; он и сложился лишь после и в значительной степени на основе появления неевклидовых геометрий (см. с. 98–111), поэтому в этой оригинальной попытке приблизить начальные понятия к природе имеется ряд неясностей и пробелов. Вместе с тем это была попытка ввести в качестве начальных некоторые топологические понятия, что свидетельствует и о положительных достижениях в стремлении Лобачевского дойти до самых глубин, до изначальных основ геометрии. Лобачевский полагал, что если приблизить начала геометрии к самой природе, то затем все выводы, полученные силой логического суждения, не смогут отклоняться от действительности, так как в разуме “как бы отпечатались первые действующие причины Вселенной, которые соглашают...все наши заключения с явлениями в природе” (см. с.62). Этот интерес к самым начальным математическим понятиям, к поискам усовершенствования начал проявился и в его работах по математическому анализу и алгебре. Он опубликовал три работы по сходимости бесконечных рядов (1834, 1835, 1841гг.). Работа 1841г. получила, как ранее и его геометрический труд, отрицательный отзыв академика М.В. Остроградского, рассмотревшего ее по поручению и министра, и президента Академии наук [7, №479, 480]. В этих трудах он проявил себя как исследователь принципиальных вопросов в области анализа, занимался актуальными проблемами своего времени. Он отчетливо разграничил понятие непрерывности и дифференцируемости, проявил глубокое понимание точного смысла понятия функция, а в своих доказательствах пользовался введенным в науку позднее понятием равномерной непрерывности. Он нашел новый признак сходимости знакоположительных рядов, доказал при весьма общих условиях теорему о разложении функции в ряд Фурье и получил некоторые результаты, предвосхищавшие дальнейшее развитие математического анализа (см. [38, с.79–86] и “Историко-математические исследования”, 1949, вып. 2, с.9–71). Одна из его работ относится к теории вероятностей (1842). В ней исследована вероятность средних результатов, полученных из повторных наблюдений, иначе говоря, найден закон распределения среднего арифметического взаимно независимых равномерно распределенных случайных величин. Эти результаты, по словам академика А.Н. Колмогорова, представляют интерес и для настоящего времени [1, т. 5, с.327–348]. В области алгебры Лобачевскому принадлежит статья о понижении степени двучленного уравнения (1834г.) и большое учебное пособие для учителей гимназии и студентов “Алгебра или вычисление конечных”, изданное им тоже в 1834г. в типографии университета. Первоначально Лобачевским была задумана и подготовлена еще в 1823г. учебная книга по алгебре для гимназии (Он сам вел преподавание в гимназии). Рукопись в окончательном виде была представлена на факультет в августе 1824г. для напечатания на казенный счет и введения ее в гимназиях. Однако по разным причинам (задержка одного отзыва, наступление событий 1825г. и др.) издание не состоялось. Осенью 1826г. Лобачевский взял рукопись обратно, выразив сожаление о напрасно затраченном труде (рукопись сохранилась и находится в библиотеке Геометрического кабинета Казанского университета. Она опубликована [1, т. 4, с.366–426]). “Алгебра” 1834г. (цензуру прошла в 1832г. [ 1, т. 4, с.5–365]) представляет собой результат переработки первоначального текста учебника и внесения существенных дополнений к нему, относящихся к высшей алгебре. По существу это – первый русский учебник высшей алгебры. Помимо своеобразного изложения известного материала и некоторых усовершенствований в доказательствах он включает ряд совершенно оригинальных результатов. Алгебра рассматривается Лобачевским как предварительное введение в математический анализ, как наука о конечном (хотя он и применяет здесь бесконечные ряды). И прежде всего алгебра “предписывает правила для счета всех чисел”. В соответствии с этой последней установкой, близкой к современной, первые восемь глав книги посвящены операциям с числами целыми и дробными и исследованию их свойств. Далее рассмотрены системы уравнений первой степени, а также решения их в целых числах; затем – степени и корни, включая операции с комплексными числами; логарифмы, их свойства и составление логарифмических таблиц (с помощью рядов); аналитическое введение тригонометрических функций; конечные разности и формулы суммирования (некоторые оригинальные), двучленные уравнения и “всякие” (т.е. высших степеней) алгебраические уравнения. Всего семнадцать глав, причем объем последней главы, возможно наиболее интересной, составляет почти одну треть книги. Мы отметим наиболее оригинальные черты этой книги. Во-первых, особое внимание здесь уделено операциям над числами и их свойствам. Далее приведен один из способов введения определителей, возникающих при решении систем, очень близких к современному (определители использованы впервые в мировой учебной литературе). Затем следует отметить чисто аналитическое введение тригонометрических функций. Это объясняется тем, что Лобачевскому важно было показать, что они могут быть определены независимо от евклидовой геометрии. Изложен оригинальный метод, позволяющий понижать степень у некоторых видов двучленных уравнений. Наконец, в последней главе найден новый способ приближенного вычисления корней алгебраических уравнений. Впоследствии он получил несправедливо название способа Греффе, хотя работа последнего вышла в 1837г. (первый вариант в 1833г.). Правда, до Лобачевского и Греффе он был предложен бельгийским математиком Данделеном в его статье 1826г. Поэтому, называя этот метод, справедливо будет упоминать имена всех трех ученых: Данделена, Лобачевского и Греффе, разработавших его независимо друг от друга. Кроме опубликованных перечисленных выше работ, в библиотеке Геометрического кабинета Казанского университета хранятся студенческие записи лекций Лобачевского за разные годы по арифметике, алгебре, геометрии, дифференциальному исчислению, дифференциальным уравнениям и механике. Имеется также большая “Записная книга” (или “Тетрадь Лобачевского”), заполненная мелко написанными математическими текстами рукой Лобачевского и начатая, повидимому, в 1821г. В ней находятся выписки из научной литературы, расчеты, связанные с подготовкой к лекциям и самостоятельные исследования, преимущественно по алгебре (все без объяснений). Кроме того, в библиотеке хранится несколько десятков отдельных листочков с заметками по физике, механике, астрономии, математике, а также и другого рода, написанными тоже рукой Лобачевского (в частности, конспективное изложение формальной логики). Это – черновые выкладки, отрывки из конспектов лекций для студентов, фрагменты самостоятельных исследований, копии стихотворений и т.п. Все эти материалы (или их описание), а также учебные планы и программы (“Обозрения преподаваний” Лобачевского) опубликованы в книге “Н.И. Лобачевский. Научно-педагогическое наследие. Руководство Казанским университетом. Фрагменты. Письма” [6], которая как бы завершает Полное собрание его сочинений, пять томов которого вышли в 1946–1951гг. Широкий круг научных интересов Лобачевского способствовал выработке им целостного материалистического мировоззрения и позволил ему высказать имеющие важное значение мысли о роли математического метода в исследовании природы. Так, построение новой математической теории, какой являлась система “воображаемой геометрии”, рассматривалось им как новая возможность более глубокого проникновения в закономерности объективного мира. В соответствии с этим он и проверял с помощью данных астрономических наблюдений применимость своей геометрии в физическом пространстве. Однако убедившись, что евклидова геометрия практически достаточно точна, и показав, как можно применить новую геометрию в математическом анализе, он как материалист высказывает уверенность, что его геометрия в дальнейшем еще потребуется либо “в тесной сфере молекулярных притяжений”, либо “за пределами видимого мира”, т.е. при расширении доступных изучению протяжений космоса, что в известном смысле подтвердилось в наше время (см. с. 121–126). Известны также его замечательные высказывания о неразрывных связях между движущейся материей и свойствами пространства. Эти связи получили конкретное выражение лишь после создания Эйнштейном частной (1905г.) и общей (1916г.) теорий относительности (см. с.117-118). Лобачевский писал: “В природе мы познаем собственно только движение, без которого чувственные впечатления невозможны. Итак, все прочие понятия, например, геометрические, произведены нашим умом искусственно, будучи взяты в свойствах движения; а потому пространство само собой, отдельно, для нас не существует...Силы все производят одни: движение, скорость, время, массу, даже расстояния и углы” [1, т. 2, с.158–160]. От математической науки Лобачевский требует, “чтобы она стала на твердом основании, чтобы строгость и ясность сохранялись в самых ее началах, так как они делаются первым ее достоинством в продолжении” [1, т. 4, с.370]. Он четко высказывается против идеалистической трактовки начал математики. “В основу математических наук могут быть приняты все понятия, каковы бы они ни были, приобретенные из природы” [7, № 244, с.204–205]. Поэтому он и предложил принять в качестве исходного геометрического понятия “прикосновение” и, опираясь на него, ввести понятие “геометрического тела”. Он был твердо убежден, что “все математические начала, которые думают произвести из самого разума, независимо от вещей мира, останутся бесполезными для математики”. В виде примера таких бесполезных начал приведены: актуальные бесконечно-малые, основания учения о движении Канта, принцип разнородности линий с углами (т.е. требование существования подобных фигур), сравнение бесконечных площадей и др. (см. там же). Он дает сжатую характеристику дедуктивного построения физико-математических наук: “...в начале их полагаются те понятия, откуда производится все учение силой нашего суждения” (см. там же). Однако, по Лобачевскому, логический вывод – это совсем не субъективное построение, в нем отражены закономерности и связи объективного мира, а именно, как он сказал в “Речи”, в началах суждения, т.е. в законах логики “как бы отпечатались первые действующие причины Вселенной, которые и соглашают, таким образом, все наши заключения с явлениями в Природе”. Это высказывание близко известному высказыванию Ф. Энгельса о познаваемости мира, поскольку мышление и познание – продукт мозга, а мозг – продукт и часть природы. Лобачевский высоко оценивает успехи физико-математических наук, называя их “славой нынешних веков, торжеством ума человеческого”. Эти успехи “справедливо удивляют нас, заставляют признаться, что уму человеческому предоставлено исключительно познавать сего рода истины. Надобно согласиться и с тем, что математики открыли прямые средства к приобретению познаний”. И далее он вкладывает в уста Ф. Бэкона уже процитированную нами (см. с.62) сжатую характеристику современного метода естествознания, опирающегося на экспериментальную проверку теории. Высоко оценивая вклад Декарта, он отмечает, что “мы живем уже в такие времена, когда едва тень древней схоластики бродит по университетам...Здесь учат тому, что на самом деле существует, а не тому, что изобретено одним праздным умом”. В этих высказываниях ясно проступает крайне отрицательное отношение Лобачевского к некоторым имевшим в то время место попыткам псевдонаучных натурфилософских построений с помощью надуманных метафизических принципов и вообще его остро критические позиции в отношении к современной ему идеалистической философии, преподаваемой в университетах. В другом месте (см. [7, № 244, с.205]) он прямо подчеркивал, что напрасно было бы искать решение трудностей построения математической науки в философии (подразумевая, конечно, современную ему кантианскую философию и особенно шеллингианскую натурфилософию, которая бралась за решение проблем всех естественных наук): “нахожу также бесполезным...искать к ним ключа в философии. Математика должна быть совершенно независима от сей науки”. Лобачевский справедливо указывает, что возможность использования математических методов в какой-либо из наук о природе – это свидетельство ее зрелости, когда качественное описание – пройденный этап, когда уже выявлены понятия и связи достаточно общие и определенные. “Все естественные науки силятся встать на ту высокую ступень совершенства, на которой последует их соединение с Математикой; и со времени сего соединения их успехи пойдут быстрыми шагами вперед. Это случилось уже с Физикой, в недавнее время с Минералогией, и есть надежда того же ожидать для всей Химии”... “Всему основанием служит справедливое понятие о вещах, которое не оставляет вести Математика через все его вычисления. После чего нет уже явлений природы, которых бы он не мог изъяснить; нет явлений, в которых бы он не мог предсказать и определить с точностью и время и меру”. И далее он особо подчеркивает, что без математики наука не сможет проникнуть достаточно глубоко в сущность изучаемых явлений. “...Но то однако ж правда, что ум, приученный к вычислениям, далеко продолжает еще итти за ту границу, которую не переступит ум, не посвященный в таинства науки чисел”. Так ярко он выразил фундаментальное значение математического метода в исследовании природы. Б.Л. Лаптев. Николай Иванович Лобачевский. К 150-летию геометрии Лобачевского. 1826-1976. - Казань: Изд-во Казанского университета, 1976. 136с. http://pyrkov-professor.ru/default.aspx?tabid=190&ArticleId=987 |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5189
Зарегистрирован: 27.08.07
|
|

Отправлено: 19.03.23 14:22. Заголовок: Весна идет-весне дор..
|  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5192
Зарегистрирован: 27.08.07
|
|

Отправлено: 19.03.23 23:26. Заголовок: Первый русский учебн..
Первый русский учебник высшей алгебры По мнению моему Алгебра первая начинает Математику со всею точностию понятий и со всей обширностию взгляда - Н.И. Лобачевский. Полное собрание сочинений. Том 4.  Настоящий четвертый том полного собрания сочинений Лобачевского содержит его работы по алгебре. Этих работ две: курс алгебры под заглавием «Алгебра или вычисление конечных», изданный в Казани в 1834г., и статья «Понижение степени в двучленном уравнении, когда показатель без единицы делится на 8», помещенная в «Ученых Записках Казанского Университета» в 1834 г. и выпущенная в том же году отдельной книжкой. Кроме того, в геометрическом кабинете Казанского государственного университета хранится рукописный первоначальный вариант «Алгебры». Этот вариант не помещен в настоящем издании целиком, так как он почти полностью совпадает с первыми 13 главами книги «Алгебра или вычисление конечных». Здесь воспроизведены лишь наиболее существенные места рукописи, которых нет в книге. В частности, рукопись снабжена интересным предисловием Лобачевского, касающимся школьного преподавания алгебры. https://www.koob.ru/lobachevskiy_nikolay_ivanovich/polnoe_sobranie_4  Предисловие из рукописи Н.И. Лобачевского «Алгебра» (1825г.) Новая книга начал Математики не должна напрасно умножать число существующих, потому что их и без того уже много. Читателю довольно слегка пробежать мою Алгебру, чтоб открыть в ней большее различие со всеми изданными до сих пор и не думать более, чтоб намерение мое было собрать и повторить только сказанное другими. Далее он не замедлит увидеть, что кроме старания сделать лучший выбор я прибавил еще и много нового. Тем более обязан оправдываться в побудительных к тому причинах, что открытия в познаниях начальных и столь обыкновенных не могли бы некому стоить больших усилий ума и мне принести чести, естьлиб с ними соединялось только новое обременение для учащихся в книге, которая назначается единственно для начинающих. Однакож я думаю иначе и скажу, что опыт на моей стороне. Два года читается Алгебра в Казанской Гимназии под моим руководством, и в последнее время я имел всю причину восхищаться успехами детей. Видел, что они тверды в правилах, понимая все, совершенно уверенные в своих знаниях, отвечают со рвением на вопросы с намерением даже сысканные, разрешают их легко, не подозревая, чтоб в них можно скрываться затруднение, достойное занять взрослых. Так, я уверился в той истинне, что понятия не должны приобретаться навыком, но должно быть переданы с первого раза во всей их обширности, с точностию, ясностию и определенностию; а потом уже утверждат[ь]ся упражнением, что[б] могли чрез то глубже напечатлеться в памяти и с легкостию быть применяемы в дальнейших исследованиях. Вот главное правило в искус[с]тве преподавать Математику, которой трудность единственно во отвлеченности и обширности понятий, которая чтоб быть легкой требует от нас только того, чтоб мы не переставали судить, употребляя знаки, как сокращения для выражения умственных представлений. Такому правилу однакож не следовали до сих пор в началах, потому что думали облегчить Учение детей, упражняя их преимущественно примерами решения задач, предоставляя им самим отвлекать для сего нужные понятия и современем только возвратиться назад, чтоб пополнить то, что было некогда сказано им недостаточно из недоверчивости к их способностям. Требование столь чрезмерное, что даже не всякой и тот мог его исполнить совершенно, кому после удавалось уходить далеко от начал. Затем готов я думать, что естьли учение Математики, столь свойственно[е] уму человеческому, остается для многих без успешно, то это по справедливости должно преписать недостаткам в искус[с]тве и способе преподавания. Не утверждая с дерзостию, чтоб я постигнул совершенство в последнем, но хочу надеяться, что избрал прямую дорогу к цели, впрочем ожидаю подтверждения от других. Говоря о способе преподавания, прибавлю еще следующее замечание, по моему мнению совершенно справедливое. Наука почти безполезная в семействах [и] весьма важная для Государств, Математика требует учения от лица Государства. Едвали не из общественных заведений могут только выходить хорошие Математики, где все благоприятствует этой науке; выбор лучших наставников, которые непрестанно трудятся увеличить собственные свои познания; порядок и строгость, так сказать военные, которые одни только в состоянии принудить учеников следовать неослабно за преподаванием и удерживать в непрестанном напряжении их внимание; наконец, множество учеников, возбуждая соревнование, рождает охоту, превращает ее современем в отрахт (sic!) и бывает причиною появления гениев — Математиков. — Нелишнее мне было здесь упомянуть об этом, потому что написал учебную книгу для Гимназии, я не боялся затруднить моей разборчивостию и строгостию в истиннах более, нежели сколько это может принести пользы. Для самой науки надобно было всегда желать, чтоб она стала на твердом основании, чтоб строгость и ясность сохранялись в самых ее началах, как oне делаются первым ее достоинством в продолжении. Такого рода опущение было вредно для целой науки, потому что было всегда причиной или без полезных исследований или темных, даже ложных понятий. — Сколько например написано защищений и возражений на всякую теорию дифференциального исчисления, в которых всего чаще можно только видеть недостаток в твердых началах и неосновательность суждений их писателей? — Лагранж в своей теории Аналитических функций старается избежать употребления бесконечно малых; между тем он не усумнился ввести в свои исчисления воображаемой корень, который сам собою не существует, а только может быть понимаем в его свойствах: последнего уже довольно. — И не должно отнимать у Математики, что служит новым средством к облегчению в ней вычислений, расширяет ее пределы, как скоро все в ней производится из начал не сомнительных. Вот почему и я говорю здесь только о воображаемых, т.е. чтоб положить первые и твердые основания вообще для всех родов вычислений, употребительных в Аналитике: главная цель Алгебры. Естьли я не напрасно трудился над сим сочинением, то за счастие быть полезным признаю себя обязанным Г. попечителю Казанского учебного округа Михаилу Леонтьевичу Магницкому, который потребовал от Профессоров его университета обратить их внимание на преподавание и поискать способов к улучшению. ***   Из обзора Н.Г. Чеботарева к сочинению Н.И. Лобачевского «Алгебра или вычисление конечных» (1834г.) В предисловии Лобачевский определяет понятие алгебры так: «В Арифметике начинают с примеров на числах; потом, соблюдая постепенность в понятиях, вместо чисел, чтобы разуметь их произвольными, в Алгебре употребляют буквы, избегая однакож способа бесконечно малых или границ, как такого, который требует более усилий от ума и составляет уже последнюю и высшую часть Аналитики» (с.23). Но дальше Лобачевский говорит: «Решение уравнений составляло всегда главный предмет Алгебры» (с.25). Для историка математики представляло бы большой соблазн из сопоставления этих двух, различных определений усмотреть предсказание характерного для алгебры XX века ее расщепления на две мало связанные друг с другом дисциплины: с одной стороны — «современную алгебру», т.е. науку о формальных операциях, развившуюся в последнее время в большую самостоятельную дисциплину, и с другой стороны — алгебру, как науку о расположении и вычислении корней алгебраических уравнений на плоскости комплексной переменной. Последняя широко пользуется методами анализа бесконечно малых, а также теорией аналитических функций. Однако можно убедиться, что здесь мы имеем дело не с предсказанием будущего явления, а с констатированием процесса, происходящего с весьма давнего времени. В самом деле, если мы обратимся к более старым авторам, то увидим, что упомянутое расщепление алгебры красной нитью проходит чуть ли не через всю историю алгебры, то усиливаясь, то ослабевая. …Какую же позицию занимал Лобачевский во взгляде на алгебру? Для выяснения этого приведем еще две цитаты из его предисловия. «В этом смысле Алгебра будет та же наука, которую Ньютон назвал Общая Арифметика, чтобы отличить от Арифметики на числах, и которую столько же справедливо можно называть вычисление конечных, в противоположность с дифференциальным или вычислением бесконечно малых, где являются неоспоримо новые начала, под каким бы видом ни старались их представлять, желая соблюсти строгость, эту существенную принадлежность всякого Математического учения» (с.23). «Алгебру и Геометрию постигла одинаковая участь (Здесь разумеется Алгебра без помощи дифференциального исчисления, так же как Геометрия без применения Аналитики - Примечание Лобачевского). За быстрыми успехами в начале следовали весьма медленные и оставили науку на такой степени, где она еще далека от совершенства. Это произошло вероятно от того, что Математики все свое внимание обратили на высшие части Аналитики, пренебрегая началами и не желая трудиться над обрабатыванием такого поля, которое они уже раз перешли и оставили за собою» (с.24). Из этих слов Лобачевского видно, что он считает алгебру пропедевтикой к высшим частям анализа и что вместе с тем он считает ее самостоятельной наукой потому, что, по его мнению, она должна разрабатывать «начала» анализа, сообщая ему необходимую строгость. Здесь нетрудно узнать ту же мысль, которая руководила Лобачевским при его работах над «началами» геометрии. Ни в одной из этих областей Лобачевский не дошел до аксиоматического метода; но потребность в нем им уже явно ощущалась. Аксиоматический метод и развился впоследствии под влиянием трудов Лобачевского. Лобачевский сперва предназначал свою книгу для гимназий; но затем, решив сделать ее пособием для учителей и студентов, значительно дополнил ее. В связи с этим можно усмотреть две различные цели, которые преследует книга: ее первые главы излагают начальные основы алгебры, причем обращается главное внимание на строгость выводов; вторая же часть книги посвящена высшим отделам алгебры, содержит много оригинальных выводов и методов и является введением в изучение дифференциального исчисления. Цель и характер первых глав прекрасно очерчены Лобачевским в следующих словах предисловия: «Всякий, надеюсь, согласится с справедливостию моего замечания, что первые понятия во всех отраслях Математических наук приобретаются легко, но всегда соединены с недостатками, которые пополнить даже и в последствии бывает весьма трудно. Если писатели для начинающих опускают это из виду, то они предполагают другую цель, опасаясь бесполезно затруднить читателей. Где-нибудь однако ж надобно воротиться снова к началам и теперь уже всю строгость почитать у места. По мнению моему Алгебра первая начинает Математику со всею точностию понятий и со всей обширностию взгляда; тогда как Арифметика составляет еще приступ, служит только приготовлением и для навыка. Вот почему в моем сочинении говорится о числах, счете, четырех действиях Арифметических. Понятие о положительных и отрицательных я не почел нужным заимствовать прямо из природы вещей, перейдя уже раз к отвлеченным; но рассматриваю их как числа, искусственно соединенные с знаками и единственно в намерении правила сложения и вычитания сделать общими» (с.24-25) ***  Представление Физико-математического отделения в Совет Университета от 18 сентября 1825г. об исходатайствовании разрешения на введение «Алгебры» в употребление в гимназиях и о напечатают ее на казенный счет. Представление подписано Н.И. Лобачевским в качестве декана отделения *** В области алгебры Лобачевскому принадлежит статья о понижении степени двучленного уравнения (1834г.) и большое учебное пособие для учителей гимназии и студентов “Алгебра или вычисление конечных”, изданное им тоже в 1834г. в типографии университета. Первоначально Лобачевским была задумана и подготовлена еще в 1823г. учебная книга по алгебре для гимназии (Он сам вел преподавание в гимназии). Рукопись в окончательном виде была представлена на факультет в августе 1824г. для напечатания на казенный счет и введения ее в гимназиях. Однако по разным причинам (задержка одного отзыва, наступление событий 1825г. и др.) издание не состоялось. Осенью 1826г. Лобачевский взял рукопись обратно, выразив сожаление о напрасно затраченном труде (рукопись сохранилась и находится в библиотеке Геометрического кабинета Казанского университета. Она опубликована [1, т. 4, с.366–426]). “Алгебра” 1834г. (цензуру прошла в 1832г. [ 1, т. 4, с.5–365]) представляет собой результат переработки первоначального текста учебника и внесения существенных дополнений к нему, относящихся к высшей алгебре. По существу это – первый русский учебник высшей алгебры. Помимо своеобразного изложения известного материала и некоторых усовершенствований в доказательствах он включает ряд совершенно оригинальных результатов. Алгебра рассматривается Лобачевским как предварительное введение в математический анализ, как наука о конечном (хотя он и применяет здесь бесконечные ряды). И прежде всего алгебра “предписывает правила для счета всех чисел”. В соответствии с этой последней установкой, близкой к современной, первые восемь глав книги посвящены операциям с числами целыми и дробными и исследованию их свойств. Далее рассмотрены системы уравнений первой степени, а также решения их в целых числах; затем – степени и корни, включая операции с комплексными числами; логарифмы, их свойства и составление логарифмических таблиц (с помощью рядов); аналитическое введение тригонометрических функций; конечные разности и формулы суммирования (некоторые оригинальные), двучленные уравнения и “всякие” (т.е. высших степеней) алгебраические уравнения. Всего семнадцать глав, причем объем последней главы, возможно наиболее интересной, составляет почти одну треть книги. Мы отметим наиболее оригинальные черты этой книги. Во-первых, особое внимание здесь уделено операциям над числами и их свойствам. Далее приведен один из способов введения определителей, возникающих при решении систем, очень близких к современному (определители использованы впервые в мировой учебной литературе). Затем следует отметить чисто аналитическое введение тригонометрических функций. Это объясняется тем, что Лобачевскому важно было показать, что они могут быть определены независимо от евклидовой геометрии. Изложен оригинальный метод, позволяющий понижать степень у некоторых видов двучленных уравнений. Наконец, в последней главе найден новый способ приближенного вычисления корней алгебраических уравнений. Впоследствии он получил несправедливо название способа Греффе, хотя работа последнего вышла в 1837г. (первый вариант в 1833г.). Правда, до Лобачевского и Греффе он был предложен бельгийским математиком Данделеном в его статье 1826г. Поэтому, называя этот метод, справедливо будет упоминать имена всех трех ученых: Данделена, Лобачевского и Греффе, разработавших его независимо друг от друга. Б.Л. Лаптев. Николай Иванович Лобачевский. К 150-летию геометрии Лобачевского. 1826-1976. - Казань: Изд-во Казанского университета, 1976. 136с. http://pyrkov-professor.ru/default.aspx?tabid=190&ArticleId=987 |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5197
Зарегистрирован: 27.08.07
|
|

Отправлено: 20.03.23 16:48. Заголовок: 21 марта 2023г., 00 ..
21 марта 2023г., 00 час 25 минут мск - Весеннее равноденствие 21 марта 2023г., 20 часов 25 минут мск - Новолуние Такоже, например, в 1833 году новолуние случилось 9 (21) Марта - Н.И. Лобачевский. Алгебра или вычисление конечных. 1834 ...Решение уравнений составляло всегда главный предмет Алгебры. В отношении к уравнениям первой степени казалось, ничего уже не оставалось прибавить после того, когда были найдены общие выражения, которые назвал я здесь представительными, для всякого числа неизвестных (Гл. IX, ст. 108). Однако ж, мне удалось такие выражения заменить собственными значениями (Гл. IX, ст. 113). Ожидаю, что такое открытие не останется без пользы. Решение уравнений первой степени в целых числах присоединил я также к Алгебре не только по тем причинам, о которых сказано выше, но желая также преподать главные основания такого учения, которое отдельно во всей обширности может почитаться затруднительным и требовать больших пособий, тогда как первые его начала делаются необходимы для самой Алгебры и могут быть применяемы в весьма обыкновенных случаях, чему примером служит решение задач из церковного счисления (Гл, X,ст. 127).    127…Церковное счисление может служить примером, чтобы видеть, как должно пользоваться свойством непрерывных дробей и решением в целых числах. Тропический год называют время, которое употребляет солнце, чтобы, описавши круг, притти снова на экватор. Это время изменяется чрезвычайно мало и в настоящем веке может почитаться в 365,24222013 дней. Синодальный месяц называется время от новолуния до другого и составляет ныне 29,5305885 дней. Помощию непрерывных дробей (Гл. VIII, ст. 84) находим к содержанию двух обращений приближенные 1/12, 2/25, 3/37, 8/99, 11/135, 19/235. Последнее, довольно уже близкое, уравнивает 19 годов солнечных с 235 лунными месяцами, и известно было еще в древности под именем Метонова девятнадцатилетнего круга. Между тем, строгое вычисление дает 19 лет…6939.60222, 235 лунных месяцев…6939.6883, а разность 0.0861 составляет один день в 221 год. … Например, в 1833 году новолуние случилось 9 Марта  - Н.И. Лобачевский. Полное собрание сочинений. Том 4. 1948г. Настоящий четвертый том полного собрания сочинений Лобачевского содержит его работы по алгебре. Этих работ две: курс алгебры под заглавием «Алгебра или вычисление конечных», изданный в Казани в 1834г., и статья «Понижение степени в двучленном уравнении, когда показатель без единицы делится на 8», помещенная в «Ученых Записках Казанского Университета» в 1834 г. и выпущенная в том же году отдельной книжкой. Кроме того, в геометрическом кабинете Казанского государственного университета хранится рукописный первоначальный вариант «Алгебры». Этот вариант не помещен в настоящем издании целиком, так как он почти полностью совпадает с первыми 13 главами книги «Алгебра или вычисление конечных». Здесь воспроизведены лишь наиболее существенные места рукописи, которых нет в книге. В частности, рукопись снабжена интересным предисловием Лобачевского, касающимся школьного преподавания алгебры. https://www.koob.ru/lobachevskiy_nikolay_ivanovich/polnoe_sobranie_4 |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5198
Зарегистрирован: 27.08.07
|
|

Отправлено: 21.03.23 00:38. Заголовок: Проективное вероятно..
Проективное вероятностное мышление
Прославление Триглава и Семерегла
Прославление Хорса златорунного и коловертящего
Древне-Славянский Зодиак
Яров день, древнерусск. ЯРОВ ДЕНЬ, тж. ЯРЬ - праздник начала Весны 21 марта 2023г., 00 час 25 минут мск - Весеннее равноденствие 21 марта 2023г., 20 часов 25 минут мск - Новолуние Се бо ящете первiе ТрiГлву покланяшете Дощ.11...Вот, возьмитесь, первое, Триглаву поклонитесь Дощечка N 11 важна для нас тем, что в ней, видимо, поучение ученику, п.ч. начало ее текста начиналось с восхваления Богу, которого автор считает троичным; он обращается к отроку, которого посвящает в великую тайну - А. Кур В февральском номере Жар Птицы 1959 А. Кур опубликовал тексты дощечек 11 (цельная), 12 (отрывок) и 13 (отрывок) (с.15-17). Всё разбито на слова и снабжено примечаниями  а рщемо Слву влiку Хрсу ЗльтРнoi КолоВртящу Дощ.12...И речем славу великую Хорсу Златорунному, Вращающему Колеса Хрсу ЗльтРнoi КолоВртящу - Хорсу златорунному, вращающему кола - Кола Времян В дощ.11 описан Древне-Славянский Зодиак, хоровод из Богов начиная с Хорса златорунного: Хърс Вльс Стрыб держетесе По за нь Вышень Леле Лiетiц Радогщ Колендо а Крышень I се о тва Удрзец Сывыi Яръ а ДажБо. Вот и почему в дощ.12 рщемо Слву влiку Хрсу ЗльтРнoi КолоВртящу И речем славу великую Хорсу Златорунному, Вращающему Колеса - т.е. с Хорса начинается отчет вращения Коло-Зодиака (у греков в начале н.э. тоже с златорунного Овна с весеннего равноденствия в марте), далее Влес (у грек. Телец), далее Стрибог (у грек. Близнецы) и соответствие с греками теряется. Вышень приходится на июнь на летнее солнцестояние. Далее в дощ.11: Се бо iны суте БiелоЯре Ладо Коупало СЪнiц Жiтнец ВЪнiц Зрнiц ОвсЪнiц Просiц Студец Ледiц а Лютец - Это по другому (по) суте - Белояр (март), Ладо (апрель), Купало (май), Сениц (июнь), Житнец (июль), Вениц (август); Зерниц (сентябрь), Овсениц (октябрь), Просиц (ноябрь), Студец (декабрь), Ледиц (январь) и Лютец (февраль).  Се бо ящете первiе ТрiГлву покланяшете Се яхом a i Тму влiкоу Слву поящехом Хвалiхом i Сварга Дiда Бжiа якожде Тено есе Родоу Божьску Нщельнiко а всенску рдоу студiц вещен яково тецЪ во лЪтЪ од крыне сва а во зме нiколеже не взмрзе А тоя воде жiвенце пiуще жiвiхомся доконе не преiдехом якожде све ко Нему убендехом до луце Егоiех раяiстiех А i Бгу Перневi ГрмоВрзецу а Бгу Пре а Боренiа ОрцЪхом Жiвента Явлены а не преставате Колiе врщате а Кii ны венде стезеоу правоу до бранiе а до Трiзнене Влiка о вся павщiа якове же iдоут ве жiвенте вЪщнiе по пълку Пруноiу А Бгу СвентоВiдiу Слву рцЪхом Се бо ста Бг Правiе a Явiе А Тому поiема песынiема яко Свт есе А чрезь Оне вiдяхом Свiет Зрящете а Яве быте А i Тоi нас о Навiе убрежешет А Тму хвлу пъiемо Пъехом плясасще Тему а взывахом Бгу нашiему якожде Тоi Земе СлонцеСуне нашiу а Звiздiа Дрезац а Свт КрiепцЪ Творяцете Слву СвiентоВiдiеве влку Слва Бгу нашiему То бо скрыбецете сердiе нашiе а се смехом одркохом сен одо злыа дЪянiа нашiа а добру тецехомсте Се бо отрце пущенiемо обыiмесе А рЪщете Се утворяiще Се бо Нь вiедЪте оуме ръзтргнещешi А по цо iсте Се бо те умiемо Се бо таiна влiка есе якожде i Сврг Перуно есе а СвентоВенд Тые Два есьва одържены о Сврзi а обаполы iа БiелоБг а ЦрнъБг сен пероутесе I Тоiе i Сврг држещете абые она Свнту не обыте пъврзещену По тоiе обасва Хърс Вльс Стрыб держетесе По за нь Вышень Леле Лiетiц Радогщ Колендо а Крышень I се о тва Удрзец Сывыi Яръ а ДажБо Се бо iны суте БiелоЯре Ладо Коупало СЪнiц Жiтнец ВЪнiц Зрнiц ОвсЪнiц Просiц Студец Ледiц а Лютец I по та Птiцец Зверенц Мiлiц Доздец Плдец Ягондец Пщелiц Тръстiц Кленчiц Езеренц Вiетрiц Сломiц Грiбiц Ловiщ Бесiедiц Снiезiц Странiц Свентiц Радiц Свiетiц Крвiц Красiц Травiц Стеблiц А за се соуте Родiц Маслiенц Жiвiц Вiедiц Лiствiц Квiецiц Водiщ ЗвЪздiц Грмiч СЪмiщ Лiпец Рыбiц Брезiч Зелiнц Горiц Страдiц Спасiц Лiствеврзiц Мыслiц Гостiц Ратiц Странiц Чурц Ръдiц А ту бо о сва ОгнБг Семьарегельi овщi а яро брзо роздено а щiстъ А то соуте ТрiГлвы обцi А се сва Онiе оде а тужде отроще одевЪрзещешi врата онiа а веiдешi во нь То бо есе красiен Раi Славьсекi А тамо Ра рiека тенце якова одЪлящешеть Сврьгу одо Яве Iа ЧенслоБг уцте дне нашiя а рещеть Бъговi ченсла сва А быте дне Сврзенiу нiже боте ноще а оусноуте Тоi бо се есе Явскi а Сыi есте во дне Бжьстiем А в носще нiкii есь iножде Бг ДiдДубСноп наш Слва Бгу Перуну ОгнКудру iже стрЪлiе на врзi вьрзе а верна предведе во стьзЪ поневжде есе Тоiе въiньм щест а соуд а яко ЗлтРоун Млств ВсПрвдьн ест Вот, возьмитесь, первое, Триглаву поклонитесь. Вот взялись мы, а и Тому великую Славу поём мы. Восхваляем и Сварга, Дида Божия, потому как Тот есть роду божьему начельник и всяческому роду родник вечный, который течет летом из крыниц (источников) своих, а зимой же никогда не замерзает. И эту воду живую пьюще, оживотворяемся, доколе не прейдем, потому как все к Нему убудем в луга Его райские. Да и Богу Перуну Громовержцу и Богу Битвы и Борения. Нарицаем (Его) Живящим Явленным, и (речем Ему) не переставать Колы (колесницы) вращать, и Который нас ведет стезею правою на брани и на тризны вликие о всех павших, кие же идут к жизни вечной по полку Перунову. И Богу Святовиду Славу речем мы. Вот, восстает (Он), Бог Прави и Яви. И Тому поем песни мы, потому как Свет есть (Он). И чрез Него видем мы Свет. Зрите - и Яви быти. А и Тот нас от Нави убережет, и Ему хвалу поем. Поем мы, пляшем Ему и взываем к Богу нашему, потому как Он Земле, Солнцу-Суне нашему и Звездам - Держатель и Света Крепитель. Творите Славу Святовиду великую. Слава Богу нашему! То ведь скорбит (скрыбецете) сердце наше, и вот мы отреклись от злых деяний наших и к Добру пришли мы с вами. Вот, отроки, с прощением (Велике Пущіння) обнимемся! И скажем: То сотворим. Вот ведь Его ведать - ум расторгнешь. А почто, воистину? Это ведь разумеем мы. Это ведь тайна великая есть, потому как и Сварог Перун есть и Святовид. (А) эти Два удерживаются во Сварге, и с обеих ее сторон Белобог и Чернобог борются. И Тех и Сварог держит, чтобы тому Свету не быть повержену. За теми Двумя - Хорс, Влес, Стрибог держатся. За ними - Вышень, Лель, Летиц, Радогощ, Колендо и Крышень. И вот за ними - Держатель Сивый, Яр и Даждьбог. Это по другому (по) суте - Белояр (март), Ладо, Купало, Сениц, Житнец, Вениц; Зерниц, Овсениц, Просиц, Студец, Ледиц и Лютец. И за теми - Птичиц, Зверенц, Милиц; Дождец, Плодец, Ягоднец; Пчелиц, Тростиц, Кленчиц; Езериц, Ветриц, Соломиц; Грибиц, Ловиц, Беседиц; Снежич, Страниц, Святиц; Радиц, Светиц, Коровиц; Красиц, Травиц, Стеблиц; А за теми - Родиц, Маслениц, Живиц; Ведиц, Листвиц, Кветиц (Цветиц); Водищ, Звездиц, Громич; Семищ, Липец, Рыбиц; Березич, Зелениц, Гориц; Страдиц, Спасиц, Листеверзиц; Мыслиц, Гостиц, Ратиц; Страниц, Чуриц, Родиц. 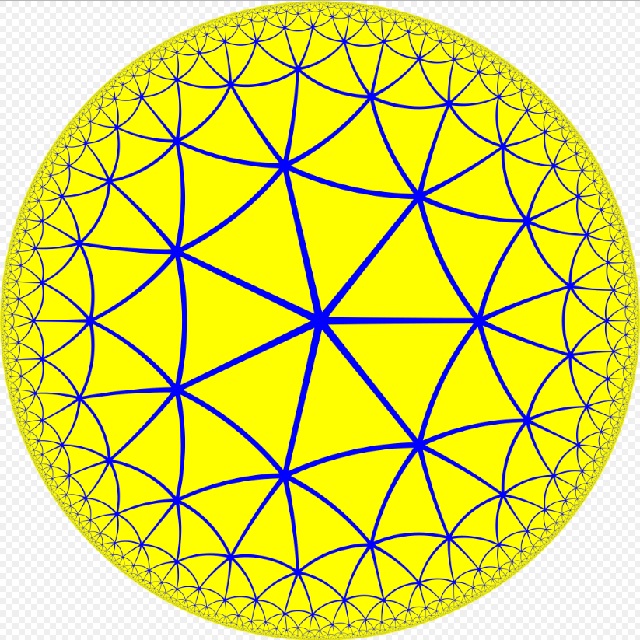 И вот для всех Огнебог Семерегл - общий и ярый, быстро рожденный и чистый.  А то (по) суте - Триглавы общие. И со всеми Ними иди. И тут-же, отроче, отворишь врата те и войдешь в них. То ведь есть прекрасный Рай Славянский. А там Ра река течет, которая отделяет Сваргу от Яви. И Числобог считает дни наши и речет Богу числа все - да быть дню небесному или же быть ночи, и уснуть. Те ведь есть Явские, и Сей есть во дне божеском. А в ночи никого нет, лишь бог Дед-Дуб-Сноп наш. Слава Богу Перуну Огнекудрому, который стрелы на врагов вержет, и верных вперед ведет по стезе, ибо есть Он воинам честь и суд, и, как Златорун, Милостлив и Всеправеден есть Влескнига, Жар-Птица и историческая память https://vk.com/doc399489626_501345325
|  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5200
Зарегистрирован: 27.08.07
|
|

Отправлено: 22.03.23 09:12. Заголовок: Влескнига. Дощечка 1..
Утреня, полдня, вечерня Слава Перуну, Хорсу и ДажьБогу Хорс златорунный и коловертящий    Аще Сурi сiашетi поемо хвлу Бгом а Огнiщу Перунiу iже есь рЪком Потятiщ на врзi А рцемо влiка Слву ОцЪм ншiм ДЪдом яковi соуте бе Сврзе Прщемо тако трiще а iдемо стд ншiх ведмо iа на трвiе Колiбо вестi iа на iнь ступе iдемо Ъстi по дроузе хвлу Бзем вознсяще Слву пьяхом а тако до плдне а рщемо Слву влiку Хрсу ЗльтРнoi КолоВртящу a сурiану пiемо а тажде до вщере А по вщере колiбо ожде огнщi сльжена заждiемо а Слву вьщернiу пьiемо ДажБу нашоi iже реком ее Прадi наше I ецымося очiсте бытi А мовлена творяще iдемо до сны а тамо влiка необiась ны... Сурье ли засиять401, поем хвалу Богам и Огнищу Перунову, Который зовется Губителем врагов402. И речем славу великую Отцам нашим, Дедам, которые суть во Сварге. И речем так трижды и идем, стада наши, ведем их на травы. Когда вести их на другую степь, идем есть, по дороге хвалу Богам вознося, славу поем, и так до полудня, и речем славу великую Хорсу Златорунному, Вращающему Колеса403, и суряну404 пьем, и так до ужина. А после ужина, когда уже огнища сложенные зажигаем, и вечернюю славу поем Даждьбогу нашему, Который речется Прадедом нашим. И идем очиститься. И, омовения сотворя, идем ко сну, и там великая необьяснимая… 401. Т.е. когда Сурья вот-вот засияет, восходя 402. „Губитель врагов" - Традиционный арийский (ведийский и авестийский) эпитет Бога-защитника, чаще всего Индры. Таким образом очевидно, что „Перун" — эпитет Индры. 403. Хрсу ЗльтРнoi КолоВртящу - Хорсу златорунному, вращающему кола - Кола Времян (ср. в дощ.11 описан Древне-Славянский Зодиак, хоровод из Богов начиная с Хорса златорунного: Хърс Вльс Стрыб держетесе По за нь Вышень Леле Лiетiц Радогщ Колендо а Крышень I се о тва Удрзец Сывыi Яръ а ДажБо. Вот почему рщемо Слву влiку Хрсу ЗльтРнoi КолоВртящу - т.е. с Хорса начинается отчет вращения Коло-Зодиака (у греков в начале н.э. тоже с златорунного Овна с весеннего равноденствия в марте), далее Влес (у грек. Телец), далее Стрибог (у грек. Близнецы) и соответствие с греками теряется. Вышень приходится на июнь на летнее солнцестояние. Далее в дощ.11: Се бо iны суте БiелоЯре Ладо Коупало СЪнiц Жiтнец ВЪнiц Зрнiц ОвсЪнiц Просiц Студец Ледiц а Лютец - Это по другому (по) суте - Белояр (март), Ладо (апрель), Купало (май), Сениц (июнь), Житнец (июль), Вениц (август); Зерниц (сентябрь), Овсениц (октябрь), Просиц (ноябрь), Студец (декабрь), Ледиц (январь) и Лютец (февраль). Интересно, что Купало приходится на май). 404. Букв. солнечную, т.е. сурицу-суру Сурьяна, древнерусск. СУРЯНА, тж. СУРЫНА - букв. солнечная, Сурьина, Сурина - сурица/ сура, квасура; тж. Сурья - Солнце. См. тж. Квасура, Сура, Сурья. Квасура, древнерусск. КВАСУРА , КВАСОУРА - напиток; тж. сура (возм. тж. "Квасуро" как имя личное). См. тж. Сура. Сура, древнерусск. СУРА, тж. СУРЕ/ СУРИЦА. Сура, сурица - алкогольный напиток, приготовляемый из ячменя сбраживанием на Солнце - СУРЕ и использовавшийся в ритуальных целях. Тж. Квасура, Суряна. Колы, древнерусск. КОЛЫ - мн. ч. колеса; круги; кола-циклы КОЛЫ СВРАЖЬЕ - Колеса (Кола) Сварженские, как олицетворение природных циклов и времени. Сварга, древнерусск. СВАРГА/ СВРГА - 1. м. р. Сварга (косв. п. ВО/ ДО СВРЗЕ/ СВРЗИ). Сварга, Небо, - то же, что Девачан, место отдыха между воплощениями, один из высших миров, "Дом неомраченного сияния". (Ср. санскр. svar-ga букв. передвигающийся по небу; ведущий на небо; небесный; небесный/ солнечный путь; m. небо; в индуизме - название одного из семи миров, в который перселяются души умерших праведников. Ср. тж. svar Солнце; солнечный свет, блеск; небо; как глагол сиять). Сварлока - пространство между солнцем и Полярной звездой, по-другому Сварга, небеса или рай Индры. расположенный на вершине горы Меру в антарикше. В текстах Влескниги архаичное слово "Сварга" чаще всего сочетается с определением МОДЕРА/ МОНДРА - синяя, голубая, лазурная; то же прилагательное употребляется и когда говорится, что Русы синеглазы (МЕДРООЧИТИЕ). Солнце, древнерусск. СУНЕ/ СУНИЕ/ СУНЬ, СУНЬЦЕ, СЛОНЦЕ, СУРЕ/ СУРА/ СУРЯ. Сурья, древнерусск. СУРЕ, тж. СУРЯ/ СУРА - Солнце, Божество Солнца (ср. санскр. surya m. Солнце; nom. pr. Бог Солнца); sura II m. Солнце; sur 1. Солнце 2. небо; герой; воин. Русы называются детьми Сурьи (в тексте дощ. 6э) - т.к. Русы - Светлые, Светоносные, также Богоносные, потому как в тексте дощ. 6г говорится: "От Них (Богов) едины мы и, раз мы Их несем, то Они у нас и есть". Вероятно, уже во время написания Влескниги слово "Сурья" было уже несколько архаичным, и для простого народа, к которому и обращается Влескнига, тут же дается объяснение: "Ведь это Солнце наше, что светит на наши дома". Николай Владимирович Слатин. Перевод, словарь имен и терминов Влескниги http://knigavelesa.narod.ru/slatin/slovar_imen_i_terminov.html Влескнига, Жар-Птица и историческая память https://vk.com/doc399489626_593063064 Утреня, полдня, вечерня Слава https://www.litprichal.ru/work/449479/ |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5205
Зарегистрирован: 27.08.07
|
|

Отправлено: 23.03.23 22:29. Заголовок: Славим Огнебога Семи..
Славим Огнебога Семирегла  Слвiхом ОгнеБга Семьiрьгла древо грызуща а сламу а огнекуде лiце розвiяштя во утiе в ден а вчерi А Тому быхом дiащi за соутворене брашно а пiтiя яко есь едiне хранiм во попелi А Того вздыiмо а горiтi... земе наше улежеся од Суна до Суна свенрожiа а влкi суте тамо бо хоросi луцi а тамо ведымо говяды а проплодiтiсе iмо волiу ДажьБу Его же славхом... ...Аж че бъ кыi вiдяi тоiя не iзесящ хвалу БозЪм трiклят буде Слава вПарунi Бгу нашiему Iжь бо ны хранящъ А такъ Бъжъ здравiю датель благi зъмны подающь Тому бъ палiм огнь вЪщень в градi НовЪ на Влховi а на горЪ у лЪсов а ть дубровЪ божъ брезы небъ дубiя понiвадiжь Бгi наше соуть в тому яко ДаЖе есь даятi просяцiм а то Ть Бъжъ хвалiхом... Славим Огнебога Семыpeгла, дерево грызущего и солому, и огнекудрое лицо развивающего и утром, и днем и вечером. И Ему даем для сотворения угощение и питье, потому как Он есть Единый, хранимый в пепле. И Его вздуваем, и горит...земля наша. Укладывается от Солнца и до Солнца Сварожьего. И велики суть там ведь хорошие луга. И там водим говяд. Да проплодиться им волею Дажьбовой. Его же славим... Если же ведь кто, зная то, не речет хвалу Богам, триклят будет. Слава Ему, Перуну, Богу нашему, Который нас ведь хранит, и таково Он — божьего здоровья Податель, и блага земные подает. Ему ведь палим мы Огонь Вечный в Граде Нове на Волхове, и на горе у лесов, либо в дубраве, у божьих берез, либо дубов, потому как Боги наши суть там, потому как Даже дает просящим, и потому Тебя, Боже, восхваляем (хвалiхом — перф. ф. 1 л. мн. ч. хвалили/ хвалим/ будем хвалить - перевод и коммент. Н. Слатина) *** Семаргл, тж. Семургло, Семерог(о)л(ов)ы, древнерусск. СЕМАРЬГЛЫ, СЬМУРЬГЛЪ, СЕМЬОРЕГЕЛЬИ - имя (эпитет), иранского происхождения, Бога огня Агни, часто выступающего как Солнце, т.е., фактически, еще один эпитет Солнца. Во Влескниге Семаргл наделен эпитетом "общий" - ведийский эпитет Агни Вайшванара, "принадлежащий всем людям", т.е. "общий для всех людей". См. тж. Агни. Агни, древнерусск. АГЕНЬ - огонь; Агни, Божество Огня (ср. санскр. agni огонь). Во многих однокоренных с санскритом русских словах звук "а" стал позже произноситься как "о", поэтому русское "акание", того типа, что мн. ч. "огни" произносится именно как древнее санскритское "агни" (кроме того, пожалуй, что "н" в такой позиции в русском произносится мягко), можно рассматривать как некое возвращение к старым произносительным особенностям. Огнебог, древнерусск. ОГНЕБЪГЪ (зват. п. ОГНЕБЪЖЕ) - эпитет Агни Бога, Бога Огня с огнекудрым ликом. Позже Огнебог назывался "Семаргл/ Семаргел" (см.). Агни-Огонь во всем, - и в небе, и в воде, и в очаге. Огнищанин, древнерусск. ОГНИЩАН - огнищан/ огнищанин, букв. "тот, у кого есть огнище", "хозяин/ владелец огнища". Огнище, древнерусск. ОГНИЩЕ - домашний очаг и Священный очаг; в отсутствие храмов или других нарочитых святилищ, обе эти функции совмещались в одном очаге. – Н.В. Слатин Вайшванара (vaicvanara букв. принадлежащий всем людям) - имя Агни, обозначающее огонь во всех его проявлениях: прежде всего на небе (солнце, молния), но также и на земле (жертвенный костер и домашний очаг), огонь вдохновения, свет среди людей, свет мысли и т.д. – Т.Я. Елизаренкова Огонь лежит в основании каждого творения. Бог есть Огонь - Е.И. Рерих *** Сему БгуОгнiкуСьмурьглЪ рцемо показатiсе а восташетiсе небесi а се взетi ож до мудра свЪта ...нарцемо Му iме iе ОгнеБъже Влескнига Дощ.3а Сему Богу Огнику Семурегле говорим мы показатися и воссташитеся на небиси, и взойти аж до мудра (синего) света...называем Ему имя Его: Огнебоже *** А ту бо о сва ОгнБг Семьарегельi Овщi а яро брзо роздено а щiстъ Влескнига Дощ.11. А вот сам по себе ОгнеБог Семьереглый (семероголовый) — общий и яро, быстро рожденный, и чистый *** Слвiхом ОгнеБга Семьiрьгла древо грызуща а сламу а огнекуде лiце розвiяштя во утiе в ден а вчерi Влескнига Дощ.31. Славим ОгнеБога Семиpeгла, дерево грызущего и солому, и огнекудрое лицо развивающего, утром, днем и вечером *** В Ригведе по представлениям ведийцев, Агни присутствовал везде: на земле, на небе и в воздухе, в воде, в камнях, в растениях, в живых существах. Признавалась также высшая форма его проявления — Вайшванара (vaisvanara- принадлежащий всем людям, т.е. всенародный), обозначавшая огонь во всех его ипостасях. *** Ригведа VI, 7. К Агни-Вайшванаре 6 Взглядом Вайшванары измерены Вершины неба, знаком бессмертного. Это на его голове (покоятся) все существа. Словно ветви, выросли семь потоков (sapta visruhah) *** Ригведа III, 5. К Агни 5 Он наблюдает за милой вершиной земли (ripa), следом птицы: Юный наблюдает за движением солнца. Агни наблюдает за семиглавым на пупе (земли). Он, возвышающийся, наблюдает за веселием богов Симфония горения https://www.litprichal.ru/work/398896/ https://www.litprichal.ru/work/442035/ https://www.litprichal.ru/work/442145/ https://www.litprichal.ru/work/442225/ |  |

|
|
|
|
Ять
|

| постоянный участник


|
Пост N: 5206
Зарегистрирован: 27.08.07
|
|

Отправлено: 24.03.23 17:08. Заголовок: Славим Огнебога Семи..
Славим Огнебога Семирегла Симфония горения  Земля в потоке быстрого солнечного ветра — происходит самая сильная магнитная буря последних лет 24 марта 2023 10:00 мск Крупная корональная дыра на Солнце причина магнитной бури 23-24 марта 2023 года. Геомагнитные обсерватории по всему миру свидетельствуют о наиболее крупной за последние несколько лет магнитной буре, происходящей сейчас на Земле и имеющей планетарный характер. Начало бури зарегистрировано около 16 часов по московскому времени 23 марта 2023 года. Пик был пройден около 2 часов ночи МКС 24 марта 2023 года. На настоящий момент (9 утра МКС) событие продолжается и, таким образом, длится уже около 17 часов. Балл бури в пике составил 7.66 по 9-баллльной шкале. Согласно международной классификации, бури такого уровня имеют следующие последствия: ложные срабатывания систем защиты в сетях электроснабжения; формирование заметного поверхностного заряда на элементах космических аппаратов, увеличение их сноса с орбиты; перерывы в спутниковой навигации и прерывания ВЧ радиосвязи. Полярные сияния могут наблюдаться до широт около 45-50 градусов, то есть, в том числе, на широтах Москвы и Санкт-Петербурга. В настоящее время уже поступают массовые сообщения о полярных сияниях на широтах от 65 градусов и выше. Буря произошла в отсутствие крупных вспышек на Солнце и вызвана исключительно редким для событий такой силы фактором — попаданием Земли в поток быстрого солнечного ветра. Такие потоки формируются на Солнце в так называемых корональных дырах — темных областях короны с открытыми линиями магнитного поля, вдоль которых происходит мощное истечение вещества в межпланетное пространство. В настоящее время исключительно крупная корональная дыра, вызвавшая бурю, непосредственно видна на фотографиях Солнца (см. изображение). Размер дыры составляет около 1 миллиона километров. Солнечный ветер представляет собой быстрый (со скоростями от нескольких сот до тысячи и более км в сек) поток солнечной плазмы, который непрерывно обдувает Землю. В обычном состоянии магнитное поле Земли находится в равновесии с этим потоком. При резком увеличении скорости или плотности потока, поле Земли выходит из равновесия и начинает колебаться. Именно эти быстрые колебания окружающего нас земного магнитного поля и представляют физическую основу магнитной бури. Механизм передачи возмущений осуществляется через возбуждение избыточных токов в проводящих телах и средах. Учитывая исключительно крупный размер корональной дыры, магнитные возмущения могут наблюдаться ещё в течение 2-3 суток, хотя и с заметными перерывами. Повышение бури до более крупных значений, чем сейчас, практически исключено, так как более сильные бури, по современным представлениям, могут формироваться исключительно после солнечных вспышек. Также маловероятен возврат пиковых значений до текущего уровня. Средний балл бури, предположительно, должен снизиться в ближайшие часы. https://tesis.xras.ru/info/20230324.html ...Отличительные черты проблемного поля, по которому проходят изыскания научной школы в ИПМ им. М.В. Келдыша РАН, — это исследование спектров структур-аттракторов как метастабильно устойчивых образований, к которым эволюционируют процессы в открытых и нелинейных средах; выявление причин локализации процессов в нелинейной среде, особенно при наличии нелинейной положительной обратной связи; исследование феномена инерции тепла, условий локализации термоядерного горения на определенной стадии. Эти научные результаты получены при изучении процессов в плазме. Здесь теоретически и экспериментально обнаружен Т-слой и изучено его применение в МГД-преобразователях энергии. Предложено другое объяснение хромосферных вспышек на Солнце. Проводится исследование процессов кумуляции, в частности, в ЛТС (лазерном теомоядерном синтезе)... Е.Н. Князева. С.П. Курдюмов. Синергетика: Нелинейность времени и ландшафты коэволюции, Изд. 2-е. М.: КомКнига, 2011. 272с. https://vk.com/doc57144397_177238171 Слвiхом ОгнеБга Семьiрьгла древо грызуща а сламу а огнекуде лiце розвiяштя во утiе в ден а вчерi А Тому быхом дiащi за соутворене брашно а пiтiя яко есь едiне хранiм во попелi А Того вздыiмо а горiтi... ...Славим Огнебога Семьирегла, дерево грызущего и солому, и огнекудрое лицо развивающего утром, днем и вечером. И Ему даем для сотворение кушанье и питье, потому как Единый храним есть в пепле. И Его вздуваем, и горит... Влескнига. Жар-Птица и историческая память https://vk.com/doc399489626_582345311 Симфония горения https://www.litprichal.ru/work/398896/ https://www.litprichal.ru/work/442035/ https://www.litprichal.ru/work/442145/ https://www.litprichal.ru/work/442225/ |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5207
Зарегистрирован: 27.08.07
|
|

Отправлено: 25.03.23 08:27. Заголовок: 🇮🇷&#..
🇮🇷🤜🇺🇸«Мы предупреждаем американского врага»: Иран угрожает США ▪️Сегодня Байден отдал приказ атаковать объекты в Сирии, связанные с иранскими силами, в связи с обстрелом американских баз в Сирии. Иранский консультативный центр в САР сделал ответное заявление: ❗️«Мы предупреждаем американского врага: у нас есть преимущество, и у нас есть возможность ответить, если наши объекты и силы в Сирии будут атакованы», – говорится в заявлении. ▪️Перед этим по базам США в САР был нанесен мощный удар двумя десятками ракет и беспилотниками, сообщается о раненых и убитых американских военных в результате обстрела базы Conaco ▪️Появились непроверенные сведения о бое между армией России и американцами в Абу-Камале Иранские ополченцы эвакуировали контрольно-пропускные пункты в районах Абу-Кемале и Маядине к востоку от Дейр-эз-Зора. "Военкоры Русской Весны" https://zmaps.ru/rvvoenkor/my-preduprezhdaem-amerikanskogo/ 01:20, сегодня  |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5210
Зарегистрирован: 27.08.07
|
|

Отправлено: 26.03.23 15:31. Заголовок: Симфония горения htt..
Симфония горения  В условиях нарастающих темпов изменений в мире, свидетелями которых мы являемся, трудно говорить о стационарных структурах, об устойчивых, неизменных образованиях, как о чем-то, лежащем в основе мироздания. Стационарные структуры самоорганизации, возникающие на стоках открытой системы, изучаемые в большинстве моделей синергетики, являются, строго говоря, тупиками эволюции! Устойчивость, хотя бы метастабильную, следует искать в динамике, а не в неподвижности во времени. В чем заключается, например, устойчивость положения велосипедиста? Оно надежно благодаря движению: пока он едет, он не падает; увеличение скорости (разумеется, до некоторого предела) ведет к повышению устойчивости его движения. В картину эволюционирующего мира вписывается представление о динамической устойчивости. Внимание исследователей нацелено на варианты стабильного развертывания нестационарных (эволюционирующих) структур, возникающих за счет нелинейных источников энергии и благодаря колоссальному ускорению процесса — обострению. Основная используемая модель, претендующая на объяснение процессов самоорганизации, образования структур и их сверхбыстрого развития, — это математические закономерности процессов горения и теплопроводности (диффузии) в открытых нелинейных средах. На активной горючей среде (с нелинейными источниками энергии), несмотря на наличие диссипативных, рассасывающих неоднородности, факторов (теплопроводности, диффузии, дисперсии, гидродинамики и т.д.), возникают и самоподдерживаются очаги горения, метастабильные структуры горения. Эта модель представляет собой одну из наиболее простых, но глубокосодержательных на современном этапе моделирования процессов самоорганизации. Огонь (или горение) справедливо рассматривать вкачестве типичного процесса, который может самовозобновляться, саморегулироваться и увеличиваться по интенсивности с драматической быстротой. Не менее впечатляющ символический и метафорический смысл образа огня. Глубокие корни метафоры горения находим в истории культуры. В Ригведе, в наиболее древнем источнике из всей ведической литературы, многочисленные гимны посвящены Агни — Богу огня. Агни — это и свет небес, разгоняющий мрак, и свет жертвенного костра, уносящего жертву к богам (как связующее звено между людьми и богами), и свет вдохновения внутри нас. Образ огня в самых различных ипостасях присутствует в буддизме, в картине космоса Гераклита, в Агни Йоге, в научно-фантастических произведениях. Однако огонь предстает в своей двуликой, внутренне противоречивой сущности. Он одновременно — неопаляющий и жгущий, спокойный и бушующий, творящий и разрушающий, концентрирующийся и растекающийся. Огонь вездесущ. А образ горения глубоко метафизичен. Человеческое тело, по сути, тоже процесс горения на открытой среде — непрерывное окисление и воссоздание. Впрочем, любой живой организм являет пример более или менее длительного горения, уничтожения, хотя бы частичного выгорания среды и ее самовозобновления, самоподдержания, роста... С.П. Курдюмов. Симфония горения http://spkurdyumov.ru/what/simfoniya-goreniya/ Ригведа X, 88. К Сурье и Агни-Вайшванаре Автор, по анукрамани, - Мурдханват из рода Ангирасов или Вамадевы (Murdhanvat Angirasa или Vamadevya). Размер - триштубх. Автор упоминает разные функции Вайшванары, постепенно расширяя их сферу действия. Это жертвенный костер (стихи 1, 4, 9), солнце (2,3,6,11,13,16), всеобьемлющее начало, пронизывающее мироздание (12, 14). Под конец гимн приобретает спекулятивный характер (17-19) - это размышление на тему о единстве и множественности Агни (18) и о возможности его постигнуть 1 Жертвенное возлияние - напиток нестареющий, приятный, Возлито в Агни, нашедшего солнце, касающегося неба. Благодаря его собственному побуждению распространились боги, Чтобы нести вселенную (и) поддерживать (ее). 2 Вселенная была проглочена, сокрыта мраком. Солнце явилось взорам, когда родился Агни. Боги, земля, небо, а также воды, Растения возрадовались в дружбе с ним. 3 Посланный сейчас богами, достойными жертвы, Я хочу прославить Агни, нестареющего, высокого, Который (своим) светом протянулся через землю И через это небо - через два мира и через воздушное пространство. 4 Кто был первым хотаром, угодным богам, Кого они помазали жертвенным маслом, выбирая (его), Тот сделал процветающим (все), что летает, что ходит, Что стоит, что движется - Агни-Джатаведас. 5 Так как ты, Джатаведас, встал во главе Вселенной, о Агни, со (своим) блеском, Мы тебя подгоняли молитвами, песнями, восхвалениями. Ты стал достойным жертв, заполняя небо и землю. 6 Ночью Агни бывает главой земли, Из него рано утром рождается восходящий Сурья. (Взгляните) же на это чудо достойных жертвы (богов), Что он быстро идет на работу, зная (свой) путь. 7 Кто приковывает взоры благодаря (своему) величию, когда его зажгут, Засверкал, возникший на небе, лучистый. В этого Агни все боги под исполнение гимнов Возлили жертвенное возлияние, (эти) защитники (наших) тел. 8 Боги создали сначала исполнение гимнов, Затем - Агни, затем - жертвенное возлияние. Он стал их жертвой, защитником (наших) тел. Его (такого) знает небо, его - земля, его - воды. 9 Этот Агни, которого породили боги, В которого совершили возлияния все существа, Своим пламенем согрел землю И это небо - (своим) величием, (он,) распрямляющийся. 10 Ведь под восхваление боги на небе породили Агни, (своими) силами заполнившего мир. Они сделали его таким, что он стал трояким. Он помогает созреть различным растениям. 11 Когда же достойные жертв боги поместили Его на небо, Сурью, сына Адити, Когда появилась бродячая пара, Только тогда все существа прозрели. 12 Для всей вселенной боги сделали Агни Вайшванару символом дней. Тот, кто протянул сверкающие утренние зори, Также раскрывает мрак, шествуя со (своим) пламенем. 13 Достойные жертвы провидцы, боги Породили Агни-Вайшванару - нестареющую Древнюю звезду, движущуюся, не сбиваясь с пути, Сильного, высокого надсмотрщика чуда. 14 Вайшванару, мощно пылающего все дни, Агни-провидца мы призываем заклинаниями, Бога, который (своим) величием охватил обе широкие (половины вселенной), Как снизу, так и сверху. 15 Я слышал о двух путях предков: (Путь) богов и (путь) смертных. На этих двух (путях) сходится все то, что движется Между отцом и матерью. 16 Две обращенные друг к другу (половины вселенной) несут странствующего. Рожденного из головы, воспринятого мыслью. Он стоит, обращенный ко всем существам, Неослабевающий, энергичный, сияющий. 17 Когда двое беседуют по эту и по ту сторону, Который из нас двоих, ведущих жертвоприношение, знает (это)? Друзья устроили общее праздничное собрание. Они достигли жертвы. Кто это провозгласит? 18 Сколько (существует) огней? Сколько солнц? Сколько утренних зорь? Сколько же вод? Без (всякого) умысла я говорю вам, о отцы. Я спрашиваю вас, о мудрые, чтобы узнать. 19 Пока прекраснокрылые (языки пламени) словно рядятся В облик утренней зари, о Матаришван, В это время действует брахман, Приходящий на жертвоприношение (и) садящийся ниже хотара. Вайшванара (vaicvanara букв. принадлежащий всем людям) - имя Агни, обозначающее огонь во всех его проявлениях: прежде всего на небе (солнце, молния), но также и на земле (жертвенный костер и домашний очаг), огонь вдохновения, свет среди людей, свет мысли и т.д. – Т.Я. Елизаренкова https://web.archive.org/web/20120428013303/http://kirsoft.com.ru/freedom/KSNews_938.htm Славим Огнебога Семирегла Слвiхом ОгнеБга Семьiрьгла древо грызуща а сламу а огнекуде лiце розвiяштя во утiе в ден а вчерi А Тому быхом дiащi за соутворене брашно а пiтiя яко есь едiне хранiм во попелi А Того вздыiмо а горiтi... земе наше улежеся од Суна до Суна свенрожiа а влкi суте тамо бо хоросi луцi а тамо ведымо говяды а проплодiтiсе iмо волiу ДажьБу Его же славхом... ...Аж че бъ кыi вiдяi тоiя не iзесящ хвалу БозЪм трiклят буде Слава вПарунi Бгу нашiему Iжь бо ны хранящъ А такъ Бъжъ здравiю датель благi зъмны подающь Тому бъ палiм огнь вЪщень в градi НовЪ на Влховi а на горЪ у лЪсов а ть дубровЪ божъ брезы небъ дубiя понiвадiжь Бгi наше соуть в тому яко ДаЖе есь даятi просяцiм а то Ть Бъжъ хвалiхом... Славим Огнебога Семыpeгла, дерево грызущего и солому, и огнекудрое лицо развивающего и утром, и днем и вечером. И Ему даем для сотворения угощение и питье, потому как Он есть Единый, хранимый в пепле. И Его вздуваем, и горит...земля наша. Укладывается от Солнца и до Солнца Сварожьего. И велики суть там ведь хорошие луга. И там водим говяд. Да проплодиться им волею Дажьбовой. Его же славим... Если же ведь кто, зная то, не речет хвалу Богам, триклят будет. Слава Ему, Перуну, Богу нашему, Который нас ведь хранит, и таково Он — божьего здоровья Податель, и блага земные подает. Ему ведь палим мы Огонь Вечный в Граде Нове на Волхове, и на горе у лесов, либо в дубраве, у божьих берез, либо дубов, потому как Боги наши суть там, потому как Даже дает просящим, и потому Тебя, Боже, восхваляем (хвалiхом — перф. ф. 1 л. мн. ч. хвалили/ хвалим/ будем хвалить - перевод и коммент. Н. Слатина) *** Семаргл, тж. Семургло, Семерог(о)л(ов)ы, древнерусск. СЕМАРЬГЛЫ, СЬМУРЬГЛЪ, СЕМЬОРЕГЕЛЬИ - имя (эпитет), иранского происхождения, Бога огня Агни, часто выступающего как Солнце, т.е., фактически, еще один эпитет Солнца. Во Влескниге Семаргл наделен эпитетом "общий" - ведийский эпитет Агни Вайшванара, "принадлежащий всем людям", т.е. "общий для всех людей". См. тж. Агни. Агни, древнерусск. АГЕНЬ - огонь; Агни, Божество Огня (ср. санскр. agni огонь). Во многих однокоренных с санскритом русских словах звук "а" стал позже произноситься как "о", поэтому русское "акание", того типа, что мн. ч. "огни" произносится именно как древнее санскритское "агни" (кроме того, пожалуй, что "н" в такой позиции в русском произносится мягко), можно рассматривать как некое возвращение к старым произносительным особенностям. Огнебог, древнерусск. ОГНЕБЪГЪ (зват. п. ОГНЕБЪЖЕ) - эпитет Агни Бога, Бога Огня с огнекудрым ликом. Позже Огнебог назывался "Семаргл/ Семаргел" (см.). Агни-Огонь во всем, - и в небе, и в воде, и в очаге. Огнищанин, древнерусск. ОГНИЩАН - огнищан/ огнищанин, букв. "тот, у кого есть огнище", "хозяин/ владелец огнища". Огнище, древнерусск. ОГНИЩЕ - домашний очаг и Священный очаг; в отсутствие храмов или других нарочитых святилищ, обе эти функции совмещались в одном очаге. – Н.В. Слатин Симфония горения https://www.litprichal.ru/work/442035/ |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5211
Зарегистрирован: 27.08.07
|
|

Отправлено: 27.03.23 06:35. Заголовок: https://i.postimg.cc..
С.П. Курдюмов и его эволюционная модель динамики сложных систем  ...В 1970-х годах научные исследования Сергея Павловича были связаны с математическим моделированием процессов термоядерного горения в плазме. Тогда было открыто, что в среде с нелинейным коэффициентом теплопроводности и объемным источником тепла процессы горения развиваются в режиме с обострением, при котором температура асимптотически уходит в бесконечность в некоторой области пространства за конечное время - время обострения. Режимы с обострением вызвали интерес ученых своими на первый взгляд парадоксальными свойствами. В нелинейной среде при определенных условиях, несмотря на наличие теплопроводности, наблюдается необычное явление - возникают области интенсивного горения в режиме с обострением, имеющие характерный размер - фундаментальную длину, в которых температура во много раз превышает температуру окружающей среды. Это феномен получил название явления локализации тепла, а области горения в режиме с обострением - нестационарными тепловыми структурами. Локализация тепла означает распад сплошной среды на отдельные структуры. Исследования, проведенные в то время группой Курдюмова, показали возможность возникновения не только простых структур, имеющих один максимум, но и сложных структур, с немонотонным распределением плотности температуры внутри области локализации, объединяющих в себе несколько максимумов. Была поставлена и решена сложная математическая задача по поиску, построению и изучению спектра сначала одномерных, а потом и двумерных структур. В 2004 году была построена первая трехмерная сложная тепловая структура в виде гантели, подобно одной из электронных оболочек атома, существование которой предсказал Сергей Павлович почти за 30(!) лет до этого. Обнаруженное явление локализации тепла открывало тогда новые подходы к решению проблемы управляемого термоядерного синтеза, и Сергей Павлович активно занимался этими задачами со своими учениками и коллегами, но на постановки задач и на результаты исследований он смотрел значительно шире. Ему было интересно: «Как, при каких условиях в однородной среде появляется организация - структуры (вихри, солитоны, диссипативные структуры), которые способны самоподдерживаться конечное время? Как они устроены и как эволюционируют во времени? Почему возникают только определенные типы структур, как устроен спектр этих структур? Как происходит «усложнение организации нелинейной диссипативной среды». И вообще: «существуют ли объективные законы эволюции, справедливые для сложных систем самой разной природы: физических, химических, биологических и даже для человеческого сообщества и самого человека, его тела, мозга и сознания?» Глубокая интуиция ученого подсказывала Сергею Павловичу, что режимы с обострением описывают процессы эволюции в сложных системах самой различной природы и обладают огромной общностью. Они возникают в нелинейных открытых диссипативных системах с положительными обратными связями. Такими системами являются автокаталитические реакции в химии, взрывные режимы в физике, механизмы свободного рынка в экономике, информационные процессы в обществе, механизмы формирования социальных сетей в интернете, в том числе в глобальной системе человеческого общества. Все эти эволюционные процессы могут быть описаны одной моделью, в основе которой лежит нелинейное уравнение теплопроводности с источником. Нелинейный коэффициент теплопроводности (диффузии) описывает диссипативные процессы в системе, распространение энергии, вещества или информации, а объемный источник описывает кумулятивные процессы, скорость прироста энергии, вещества или информации в системе. Аккумуляция и диссипация - две важнейшие динамические составляющие процессов в сложных системах, а их единство есть движущая сила эволюции. Нелинейная динамика сложных систем разного типа может быть рассмотрена единым образом, с точки зрения развития и взаимодействия структур разной сложности, развивающихся в режиме с обострением. Исследованию синергетических свойств режимов с обострением и особенностей формирования нестационарных диссипативных структур, обобщению, осмыслению, новой интерпретации полученных результатов Сергей Павлович посвятил всю оставшуюся жизнь. Он занимался, по его собственному признанию, «поиском истины мира в режимах с обострением». И в мировую науку С.П. Курдюмов внес наибольший вклад именно как исследователь режимов с обострением и сложных структур, возникающих и эволюционирующих в режимах с обострением. Созданная им модель тепловых структур - одно из его важнейших достижений. ...Если подняться на междисциплинарный уровень и отвлечься от конкретной природы системы, можно установить общие законы эволюции нелинейного мира, строя модель развития пространственно-временных структур в сложной системе. Для эволюции систем, развивающихся в режиме с обострением, характерны: а) наличие нескольких стадий; б) ускорение развития со временем, выражающееся в сокращении длительности стадий и наращивании общего темпа развития; в) усиление неустойчивости развития; г) изменение характерных размеров структур. Последняя стадия эволюции - это взрывное развитие (blow-up), заканчивающееся коллапсом или радикальным поворотом с рождением природных, социальных или культурных инноваций. На определенной стадии структуры могут формироваться, на других стадиях распадаться, существуют периоды устойчивого быстрого роста и периоды кризисов, дезинтеграции структур, которые с неизбежностью заканчиваются формированием новых структур. Первая публикация с претензией на новое мировидение, опирающаяся на изучение процессов, развивающихся в режиме с обострением, была сделана Курдюмовым в 1979 году. Это был препринт Института прикладной математики им. М.В. Келдыша, который назывался «Собственные функции горения нелинейной среды и конструктивные законы построения ее организации» [7]. В этой работе, подводя итог многолетних исследований и анализируя свойства решений нелинейного уравнения теплопроводности, описывающих формирование и развитие диссипативных структур в плазме, Курдюмов вводит несколько основополагающих понятий, которые разовьет в дальнейшем в своих работах с Князевой. Во-первых, это понятие собственных функций нелинейной среды - строго определенного, дискретного набора пространственно-временных структур, которые могут формироваться и развиваться в данной нелинейной среде. Во-вторых, это понятие темпомира структуры (термин, введенный им вместе с Князевой), связывающего возраст структуры со скоростью (темпом) ее развития [6]. В-третьих, это принцип объединения простых структур «разного возраста» в единую сложную структуру. В-четвертых, это идея немонотонного циклического развития, которую впоследствии он с В.А. Белавиным впервые применяет к глобальной демографической системе [8,9]. При этом в качестве ключевых выступали, по меньшей мере, три мировоззренческие идеи, а именно: идея о связи пространства и времени, идея о сложности и ее природе (стремление понять, что есть сложность и каков путь к сложному) и идея циклов и переключения режимов как необходимого механизма поддержания «жизни» сложных структур. ...Рассмотрим, как происходит формирование структур на ранних стадиях эволюции из достаточно произвольных начальных распределений. Расчеты показали, что вначале за счет процессов диффузии идет глобальная перестройка профиля начального распределения, которая может сопровождаться его значительным растеканием (см. рис.7). Затем растекание прекращается и начинается формирование и рост одной, двух и более простых или сложных структур. 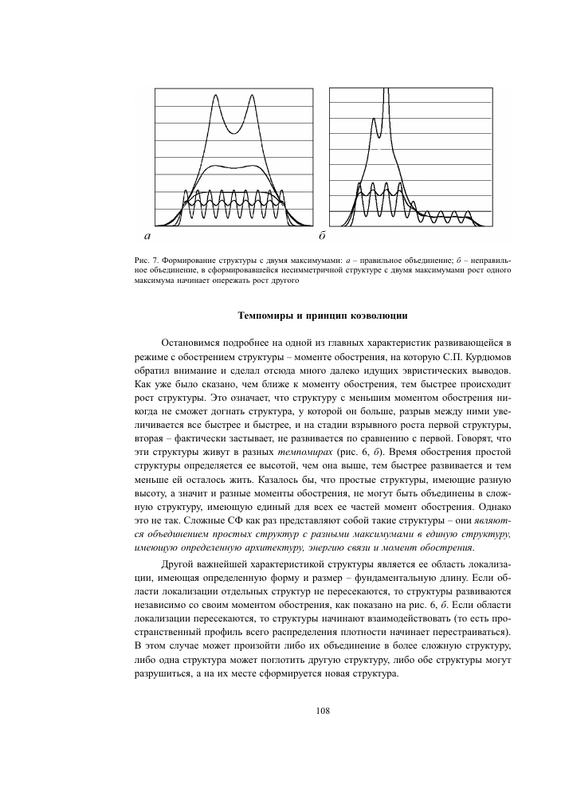 На рис.7а показано формирование структуры с 2-мя максимумами из начального синусоидального распределения плотности, имеющего много максимумов. Сформировавшаяся СФ (собственная функция) развивалась по автомодельному закону почти до момента обострения. На рис.7б показан пример другого расчета, в котором образовалась несимметричная структура с двумя максимумами, которая жила недолго, потому что не соответствовала симметричной СФ. В итоге более высокий максимум оторвался от меньшего максимума и стал развиваться в более быстром темпе; он и определил динамику развития всей структуры. Таким образом, для данной нелинейной среды с заданными параметрами существует строго определенный набор пространственных конфигураций, в которые можно объединять простые структуры, и этот набор определяется спектром СФ. Совокупность всех сложных СФ, развивающихся в одном темпе или «живущих» в одном темпомире, представляет собой организацию нелинейной среды. Иными словами, сложные СФ являются «правильным» объединением простых структур с разными максимумами, при котором все части структуры развиваются синхронно в одном темпомире. В этом состоит выдвинутый С.П. Курдюмовым принцип коэволюции, принцип нелинейного синтеза или принцип объединения простых структур в сложные [7]. Модель эволюционной динамики С.П. Курдюмова В последнее время стало ясно, что режимы с обострением, описывающие развитие во взрывном режиме, являются промежуточными асимптотиками очень многих реальных процессов, и уравнение (1) обладает большой общностью. Доказано, что оно является асимптотикой многих уравнений с другими зависимостями k(Т) и Q(Т) [10]. В режиме с обострением происходила химическая эволюция во Вселенной, биологическая эволюция, глобальная эволюция общества, а также развитие многих крупных и мелких физико-химических, биологических, социальных, экономических и других систем. Для эволюции систем, развивающихся в режиме с обострением, характерен ускоренный рост общей мощности рассматриваемого процесса, который выражается в сокращении периодов, или циклов развития [27-30]; усиление процессов концентрации вещества или информации в некоторых центральных местах [31]; формирование, развитие структур разной сложности и их гибель на заключительных этапах циклов. Все это имеет место в LS-режиме с обострением и адекватно описывается уравнением (1). Многие общие законы пространственно-временной эволюции систем могут быть выведены из динамики режимов с обострением и описаны с точки зрения развития сложных структур. Именно динамика режимов с обострением была положена С.П. Курдюмовым в основания синергетики [1-3]. Поэтому уравнение (1) мы назвали моделью эволюционной динамики С.П. Курдюмова. С.П. Курдюмову принадлежит идея применения этого уравнения и для моделирования эволюции человеческого сообщества. Он увидел глубокую аналогию между процессами горения нелинейной среды, ведущими к образованию и распаду сложных пространственно-временных структур, и историческими процессами, сопровождающимися образованием, ростом и распадом империй [8,9]. Новые результаты по моделированию глобальных исторических процессов получены в работах учеников и продолжателей дела Курдюмова [33-38]. В этих работах были исследованы основные тренды и исторические циклы развития, проанализированы особенности расселения людей и развития пространственных структур: городов, государств, империй, геополитических и экономических сообществ на каждом историческом этапе, сопоставленным с этапом развития в режиме с обострением, определены некоторые черты будущей цивилизации. Важнейшими следствиями анализа эволюционной динамики в режиме с обострением являются следующие выводы: • о метастабильной устойчивости структур социального мира; • об усилении неустойчивости в моменты максимального развития, расцвета (приближении к моменту обострения); • о периодическом распаде сложных структур и формировании новых структур, возникновении социальных и культурных инноваций; • об усилении дифференциации, расслоения в социальных структурах и выпадения самых слабых звеньев из общей развивающейся структуры. Понимание законов эволюции и коэволюции, а также синергетических принципов управления сложными системами позволяет оказывать влияние на выбор благоприятных путей развития в точках бифуркации или вблизи обострения, формирование предпочтительных сложных структур и поддержании их метастабильной устойчивости. Поиск конструктивных принципов коэволюции сложных структур мира - главное дело жизни Сергея Павловича. Почему открываемые синергетикой принципы коэволюции Курдюмов называл конструктивными? Потому что они могут использоваться для эффективной управленческой деятельности в социуме, для стратегического видения будущего и планирования на долгосрочную историческую перспективу, для выработки разумной национальной и государственной политики в глобализирующемся мире. Потому что синергетические принципы коэволюции глубоко содержательны и ориентированы на отдаленное будущее, которое практически невозможно предсказывать традиционными методами. Потому что глубокое понимание синергетических принципов коэволюции, нелинейного синтеза частей в устойчиво эволюционирующее целое может и должно лечь в основу современного «искусства жить вместе», содействуя утверждению толерантности и сохранению разнообразия в глобализирующихся сообществах. Коэволюция, как учил Курдюмов, есть «искусство жить в одном темпомире», не свертывая, а поддерживая и развивая разнообразие на уровнях элементов и отдельных подсистем.  Круглый стол по синергетике. Москва, 1996 Во втором ряду стоят слева направо: пятый слева С.П. Капица, В.А. Белавин, Г.Г. Малинецкий, С.П. Курдюмов, ?, В.Г. Буданов, В.А. Копцик, Ю.Л. Климонтович, И.А. Акчурин. В первом ряду сидят, слева направо: И.В. Мелик-Гайказян, ?, Е.Н. Князева. Куркина Е.С., Князева Е.Н. - С.П. Курдюмов и его эволюционная модель динамики сложных систем // Известия вузов. ПНД. 2013. Т. 21, вып. 4. с.135-217 https://andjournal.sgu.ru/ru/articles/s-p-kurdyumov-i-ego-evolyucionnaya-model-dinamiki-slozhnyh-sistem https://cyberleninka.ru/article/n/s-p-kurdyumov-i-ego-evolyutsionnaya-model-dinamiki-slozhnyh-sistem |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5213
Зарегистрирован: 27.08.07
|
|

Отправлено: 27.03.23 19:05. Заголовок: Вести из будущего Пр..
Вести из будущего Программа "СИНЕРГЕТИКА" в цикле А. Гордона С. Курдюмов, Г. Малинецкий запись 17 марта 2003 года https://www.youtube.com/watch?v=-ZN_4BAfLM4&t=22s см. 41:41- Сергей Курдюмов: Это верно. Я хочу это поддержать. Но ещё сказать и о некоторой особенности. Это всё палиатив такой. Надо знать где кризис, нужно строить сейсмически устойчивые здания, нужно предсказывать, чтобы потратить в десять раз меньше на восстановление чего-то, а лучше на предупреждение. Нужно сберечь людей, нужно, так сказать, лечить их более правильно. Но есть ещё более глубокие задачи, которые всегда где-то в глубине души у наших слушателей, да и у нас тоже, таятся и говорят, что мы всё-таки сверхсложных проблем, которые за всем этим прячутся, не решим. Всё равно неизвестно, как мы будем жить вместе с природой, мы же её уничтожаем! За год мы уничтожаем то, что природа накопила в виде угля, нефти, газа за несколько миллионов лет. Разве можно так долго существовать? Есть такие вопросы, которые отодвигаются, а не решаются. Мы говорим об экологии, что нужно делать очистные сооружения. И все это понимают, что их нужно делать. Сложно добиться этого особенно в развивающихся странах. Ну, в конце концов, при мощном воздействии средств информации, образования, выравнивания уровня жизни, которое происходит во всём мире. Сейчас мы имеем золотой миллиард, но он долго не продержится, он будет выровнен. Это определённая стадия развития. И всё-таки останутся вот эти нерешённые сверх-кардинальные вопросы: как устойчиво жить вместе? Устойчиво не означает без кризисов. Это пустяковое утверждение наших горе-политологов, что больше революций не будет, больше кризисов не будет. Мир – это сложный нелинейный объект, а также обязательный кризис, обязательная бифуркация, обязательно выбор. Психологи говорят о человеке, как о сверхсложном объекте, который всё время делает выбор: куда пойти, что сделать. Непрерывный выбор. Время человеческого разума идёт в другом темпе. Без выбора сложное не существует. Как найти нить Ариадны, которая бы открыла далёкое будущее, а не чуть-чуть отодвинутое дальше. Ну, конечно, загадывать вперёд – это опасно. Мы в институте прикладной математики занимались управляемым термоядерным синтезом, сначала неуправляемым, потом управляемым. Оттуда, кстати, и пошли многие нелинейные задачи, которые ищут новые принципы, новый необычный подход, роль хаоса в системах, способ их прохождения, а также они объясняют очень много явлений современной культуры на современной стадии развития. Это не означает, что дальше всё погибнет, что будет всеобщая катастрофа. Погибнуть можно. Всё сложное смертно. Но это не железный барьер, который непреодолим. На самом деле, есть пути в будущее и после этой хаотической стадии. Есть ещё более поразительные вещи, связанные с оценкой будущего. Они такой же мощности, как специальная теория относительности. Вот я просто привожу пример. В своё время, во всех европейских гостиных многих государств, дамы в кринолинах интересовались новым понятием времени, тем, как можно попасть в будущее. Помните, близнецы. Один из них очень ускорен, до скоростей близких к скорости света, а потом он возвращается. У того близнеца прошли десятилетия, а у этого прошли всего несколько часов. То есть можно попасть в своё собственное будущее. И многие другие вещи. Они, правда, проявляются вблизи больших скоростей. А оказалось, что есть общая особенность в развитии нелинейных систем и специальной теории относительности. Это нелинейная система, у которой, например, масса ускоряемой частицы так возрастает, что при изменении скорости до скорости света она увеличивается до бесконечности. Приблизительно так же, как растёт население в течение сотен тысяч лет. Это доклады Капицы. Ну, конечно, никаких бесконечностей не бывает. Есть та особенность, которую сейчас человечество проходит. Демографический кризис, очень сильный рост населения, сопровождающийся ростом науки, культуры, потому что население нужно кормить, обеспечивать, это единое системное тело общества. А мы знаем, что пройти его можно. Но это кризисное состояние, это срыв на увеличение доли хаоса, на разравнивание, как мы говорили. И при этом проявляются замечательные особенности. Вблизи этих резких процессов, резких изменений, оказываются модели, которые, описывая эти процессы, колоссально упрощаются. Вопрос, как прогнозировать развитие общества? Откуда вы возьмёте модель? Для того, чтобы предсказать пути развития нужны правильные структуры. Не единичные структуры, а несколько, выбор структур. А оказывается, что вблизи моментов обострения колоссально упрощаются модели, и это приводит к совершенно замечательным результатам. В специальной теории относительности есть связь, особая связь – пространство и время. Ну и есть пространственно-временная длина, инвариант такой. Что нового появляется в сложных системах, таких как общество и человечество, в смысле связи пространства и времени? Один из интереснейших вопросов. Вот синергетика показывает, пока на частных случаях, и вместе с ней термодинамика режимов с обострением, что появляется связь с будущим. Мы привыкли думать, что развитие системы определяется только прошлым. Ну, и то не всем прошлым, а тем прошлым, которое в той или иной степени воздействует, помнится, а не стирается. Что-то из прошлого исчезает, конечно, есть задний фронт воспоминаний. Хотя психика, например, человека содержит видовые рефлексы, половые, пищевые и так далее, уходящие в глубину эволюции. Оказывается, что в сложных системах таких, как человечество и человек, проявляется влияние будущего. Самый простой пример это то, что разные страны находятся на разных уровнях развития. На разных стадиях развития. Есть аборигены, которые относятся почти к родовому обществу где-нибудь в Африке, и есть посткапитализм в Америке, есть постсоциализм в Китае и европейский постсоциализм. Понимаете, и они действуют друг на друга. Но в человеке, как показала целая серия вышедших сейчас статей, есть странная вещь, – оказывается, что в человеке есть влияние абсолютного будущего. То есть в каких-то участках сложной структуры процессы сегодня происходят как в прошлом, а в других участках сегодня при определённых условиях, при автомодельных установлениях происходят как в будущем. Как будут во всей структуре происходить в будущем. Это есть то принципиальное отличие, которое отличает его от специальной теории относительности. Но оно такой же мощности. Оно позволяет думать, что мы не только управляемся прошлым, но есть и влияние будущего. Что это такое? Одна из интереснейших тайн. https://spkurdyumov.ru/video/est-li-budushhee-u-nauki-programma-a-gordona-efir-17-03-2003-s-p-kurdyumov-g-g-malineckij/ https://www.intellect-video.com/1504/Gordon-Sinergetika-online/ В. Хлебников. Открытие Народного университета Отчет Вчера в Народной аудитории в присутствии будущих слушателей и всех сочувствующих делу народного образования состоялось открытие Высшей вечерней школы. Товарищ Бакрадзе познакомил присутствующих с задачей нового очага знаний - дать возможность рабочим посвятить просвещению свой вечерний отдых. Выступившие с речами пр(офессора) Усов и Скрынников познакомили со взглядами современной науки на происхождение жизни на земле и влияние земного шара на земные существа. Было прочитано несколько приветствий, в том числе от учащихся средней школы Мысли по поводу В вступительном слове тов. Бакрадзе отметил, что, создавая высший вечерний храм знания, рабочая власть открывает доступ к Солнцу Науки для тех, чьи сутки делятся на три равные части: труда, отдыха и сна - и, будучи занят днем, должен посвятить жажде знания свой вечерний отдых. Рабочих, до сих пор изгнанных, имела в виду пришедшая на смену царскому праву рабочая власть. Пусть все, кто видел храм науки в узкую щель, войдут в его широко распахнутые двери! Какие бы скачки ни делал путь мировой свободы, ничто не может грозить таким памятникам рабочего права, как только что открытый вечерний храм науки. Здесь путь, взятый рабочей властью, безошибочен. Проф. Усов произнес слово о происхождении жизни на земле. Он указал, что мельчайшая жизненная пыль могла быть занесена на землю теми небесными камнями, какие с таким треском и шумом пролетают над землей. Это своего рода небесная почта, и каждый такой камень падает как письмо с соседней звезды. Не дело ли Человека Будущего это несовершенное детище природы взять в свои руки и молотом рабочего построить правильные сношения с соседними светилами, вероятно, тоже населенными, пусть и не людьми? Думалось, может быть, правы те, кто хотят увенчать великую войну завоеванием Месяца. Пока же вести оттуда долетают до нас как небесные камни. Проф. Скрынников посвятил свою речь первым шагам жизни на земле. Вести из будущего осаждали сознание. Невольно мысль переносилась в будущее, когда рука рабочего построит подводные дворцы для изучения глубин моря, на горе Богдо гордо подымется замок для исследования неба Лебедии - осада человеческим разумом тайн звездного мира, бесчисленные колодцы, вырытые в пустыне, покроют сыпучие пески садами и зеленью, напоминая чудеса, достигнутые французами в Сахаре, и стройный тополь привяжет к месту сыпучие пески устья Волги, так напоминающ(ее) Бельгию, (оно) станет одним цветущим городом, одной, покрытой садами, общиной-задругой, на пути к единой общине земного шара. Думалось, что у устья Волги встречаются великие волны России, Китая и Индии и что здесь будет построен Храм изучения человеческих пород и законов наследственности, чтобы создать скрещиванием племен новую породу людей, будущих насельников Азии, а проследование индусской литературы будет напоминать, что Астрахань - окно в Индию. Думалось о том времени, когда единая для всего земного шара школа-газета будет разносить по радио одни и те же чтения, выслушиваемые через граммофон и составленные собранием лучших умов человечества, верховным советом Воинов Разума. Был прочтен привет от будущего, от учащихся средней школы 1918 https://web.archive.org/web/20121231211912/http://sinsam.kirsoft.com.ru/KSNews_215.htm |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5214
Зарегистрирован: 27.08.07
|
|

Отправлено: 28.03.23 08:00. Заголовок: Пламень созидающий
Пламень созидающий  Матаришван (mataricvan) - мифологический персонаж, похитивший в изначальном мире огонь для богов и для Ману Ригведа. Из словаря основных мифологических персонажей и ритуальных понятий. Составила Т.Я. Елизаренкова Молiхомь Патаре Дiаiе яко Тоi iзведе огнь iждеть МатырьСваСлава прiесеть на крыдлiех све ПраОцем нашiем i клiщеть МатрСва до Вшнiего яковье даял есе еiе огень до огнiцы нашiе Пiсне хвалы а Матыря спѣваще Тоя красна Птыцiя яква несе ПраЩурем нашем огнь до домы iа... Влескнига *** Горение (или огонь) можно рассматривать, пожалуй, в качестве одного из архетипических символов - символа самовозобновляющегося и саморегулирующегося начала в универсуме. *** ...Даже относительно простые модельные нелинейные уравнения с нелинейными источниками и стоками (которые отражают особенности открытых систем) описывают очень сложное поведение: содержат большое число типов структур, к которым при разных начальных воздействиях идут процессы. Благодаря общности математического описания многих процессов различной природы мы усматриваем новый смысл в метафорических моделях мира древних мыслителей. Так, огонь уже тысячелетия назад считался одной из основных сил природы, наряду с водой, воздухом и землей. Образ огня или горения выступал в качестве объяснения законов развития мира. Математические закономерности процессов горения и теплопроводности (диффузии) на современном этапе представляют одну из наиболее распространенных моделей, претендующую на выяснение многих парадоксальных процессов синергетики. Последние связаны с возникновением на активной (горючей) среде локализованных (несмотря на наличие теплопроводности) очагов горения (химических реакций) - диссипативных структур. Имеется в виду исследование образования и эволюции структур горения и тепла в открытых и нелинейных средах. Результаты на уровне математических теорем получены на ограниченном классе уравнений - на уравнениях параболического типа, то есть типа теплопроводности, квазилинейных, с источником, хотя некоторые выводы уже распространены на другие классы нелинейных уравнений в частных производных. Следует подчеркнуть, что здесь рассматриваются диссипативные структуры существенно нестационарные, пульсирующие, усложняющиеся и деградирующие и т.д. За пределами нашего внимания в этой статье остаются другие, не менее важные и не менее интенсивно разрабатываемые поля исследований, а именно - стационарные структуры (также являющиеся аттракторами* процессов самоорганизации), бегущие волны, в первую очередь, солитоны. Кроме того, сама нестационарность может быть по-разному понята. Нестационарность - характеристика не только структур, но и состояний сред, в которых не успевает устанавливаться равновесие и которые описываются кинетическими уравнениями. Кинетические нелинейные методы также остаются вне нашего рассмотрения. То есть мы говорим о синергетике, изучая область нелинейных уравнений определенного класса. Как правило, вызывает недоверие или даже шок то обстоятельство, что простые математические модели, причем модели определенного, ограниченного типа, могут содержать фундаментальные результаты, что заложенные в эти модели идеи могут выходить далеко за пределы их конкретного содержания. Разъясняя большую общность и фундаментальность данных результатов, стоит особо подчеркнуть прежде всего глубинную метафоричность образа горения. Это типичный образ быстроразвивающегося процесса вообще. Горение (или огонь) можно рассматривать, пожалуй, в качестве одного из архетипических символов - символа самовозобновляющегося и саморегулирующегося начала в универсуме. Архетипический образ горения развертывает перед нами американский филолог Ф. Уилрайт. Он обращает внимание на то «свойство огня, которое всегда будоражило людское воображение и не поддавалось рациональному объяснению: его кажущаяся способность к самопроизвольному зарождению и быстрому самовоспроизведению. С древнейших времен люди замечали с благоговейным ужасом, что огонь может возникать в результате внезапного воспламенения и что его размер и интенсивность могут увеличиваться с драматической быстротой [выделено нами. - Авт.]» [34. с.102]. В Ригведе, самой древней из всех Вед, многочисленные гимны посвящены Агни - богу огня. Агни - это небесный огонь, связанный с бесчисленными огнями на Земле. Агни-Вайшванара, то есть «принадлежащий всем людям», - это огонь во всех своих проявлениях: это свет небес, разгоняющий мрак; свет жертвенного костра, уносящего жертву к богам; свет среди людей; свет вдохновения внутри нас [см. 28. с.278-279]. Рождения и превращения Агни самообусловлены. Агни, «(своими) силами заполнивший мир» [28. с.109], - это, по сути, не вполне явное, но уже присутствующее выражение субстанциального начала как causa sui. В 14-томной Агни Йоге, созданной Е.И. Рерих и Н.К. Рерихом и оставленной ими безымянно принадлежать культуре, образ огня, пожалуй, центральный. «Стихия Огня, самая вездесущая, самая творящая, самая жизненосная, менее всего замечается и оценивается, - читаем мы в первых строках «Мира Огненного». - <...> От обычных световых образований, доступных открытому глазу, до сложных огней сердца - все вводит нас в область Огненного Мира» [Мир Огненный. I, 1]. Причем огонь предстает в философии Агни Йоги в своей амбивалентной сущности: он одновременно неопаляющий и жгучий, спокойный и бушующий, творящий и разрушающий, концентрирующийся и растекающийся. Образ огня в различных ипостасях используется в буддизме. Как отмечает О.О. Розенберг, «буддисты сравнивают бытие с лампадой и с океаном. Горящая лампада с мигающим волнующимся пламенем, т.е. бытие, погаснет наконец, прекратится процесс горения, лампада же остается. Океан бушует, охваченный бурей, но буря наконец стихает, и волны замирают, океан в покое, однако это не значит, что океана нет» [29. с.29]. Здесь подчеркивается цикличность рождения многочисленных бытийных проявлений огня из Небытия, из первородной хаотической, потенциально свертывающей в себе все и спокойной прасреды, и возвращение в нее вновь. Стоит сослаться здесь также на известный образ огня в картине Космоса Гераклита, огня как меры самовозобновления и самоугасания процессов в нем. «Этот космос, один и тот же для всего существующего, не создал никакой бог и никакой человек, но всегда он был, есть и будет вечно живым огнем, мерами загорающимся и мерами потухающим» [20. с.44]. Огонь вездесущ. А образ огня глубоко метафоричен. Человеческое тело ведь, по сути дела, представляет собой процесс горения, процесс непрерывного окисления и воссоздания, сохранения своей целостности, происходящий на открытой среде. Впрочем, любой физический организм являет нам пример более или менее длительного процесса горения, процесса уничтожения, выгорания, хотя бы частичного, среды и ее самовозобновления, самоподдержания, роста. Отождествление огня и жизни восходит к учению прославленного врача и натурфилософа эпохи Возрождения Парацельса. Он считал, что там, где есть огонь, есть и источник жизни, ее порождения и исцеления, поскольку огонь символизирует имманентно присущее бытию свойство становления. Французский философ Гастон Башляр изучает двуликую и противоречивую природу огня и особенности его образа огня в человеческом разуме. Он справедливо отмечает, что огонь преподает человеку урок глубины становления [5. с. 89]. Это и внешний для нас огонь-разрушитель, поглощающий жизнь и сложную организацию, и внутренний, интимный огонь-созидатель, творец жизни и ее новых форм. Это и то, что мы имеем, что мы переняли и пытаемся сохранить, и то, что существует в нас имманентно благодаря нашей внутренней природе, огонь собственного становления и расцветания, личностного роста, который можно лишь обнаружить и которому можно лишь дать возможность разгореться с драматической быстротой. «Созерцатель огня видит в нем образ изменения - стремительного и наглядного. Огню не свойственно абстрактное однообразие водного потока; он растет и меняется быстрее, чем птенец в гнезде среди кустов, за которым наблюдаешь изо дня в день, - и потому он вызывает жажду перемен, желание ускорить время, подвести всю жизнь к завершению, к пределу потустороннего. Такая мечта, поистине захватывающе-драматичная, расширяет горизонты человеческой судьбы, связывает малое с великим, очаг с вулканом, существование куска дерева с бытием целого мира. Зачарованный человек слышит зов огня. В разрушении ему видится нечто большее, чем просто изменение, - обновление» [5. с.32]. Все эти образы огня в культуре созвучны с развиваемыми в данной статье синергетическими представлениями о формировании и эволюции структур горения в открытых и нелинейных средах. И, по большому счету, через эти представления просматриваются универсальные принципы эволюции нестационарных структур в целом. * Аттрактор - устойчивое состояние (структура) системы, которая как бы «притягивает» (от лат. attrehere - притягивать) к себе все множество «траекторий» системы, определяемых различными начальными условиями (если система попадает в конус, или сферу, аттрактора, то она неизбежно эволюционирует к этому устойчивому состоянию/структуре). Тогда как в большинстве работ по проблемам самоорганизации под аттрактором понимается изображение этого относительно устойчивого состояния в фазовом пространстве, в настоящей работе аттракторами называются реальные структуры в открытых нелинейных средах, на которые выходят процессы эволюции в этих средах в результате затухания промежуточных, переходных процессов. Подчеркивая это, мы часто употребляем целостное новообразование «структуры-аттракторы». Е.Н. Князева, С.П. Курдюмов. Синергетическая парадигма. Основные понятия в контексте истории культуры. 2005 (Если искать предельно краткую характеристику синергетики как научной парадигмы, то такая характеристика включила бы всего три ключевые идеи: самоорганизация, открытые системы, нелинейность. Синергетика изучает механизмы самоорганизации определенного класса систем (открытых и нелинейных) самой различной природы, начиная с физики и кончая социологией и загадками человеческого Я, системой его сознания и подсознания). https://cyberleninka.ru/article/n/sinergeticheskaya-paradigma-osnovnye-ponyatiya-v-kontekste-istorii-kultury
|  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5216
Зарегистрирован: 27.08.07
|
|

Отправлено: 29.03.23 08:55. Заголовок: Матер-Сва-Слава Вся ..
Матерь СваСлава и Матаришван  Молiхомь Патаре Дiаiе яко Тоi iзведе огнь iждеть МатырьСваСлава прiесеть на крыдлiех све ПраОцем нашiем Дощ.19 Молимся мы Питару Дию, потому как Он низвел Огонь, который Матерь Всех Слава приносит на крыльях своих Праотцам нашим. i клiщеть МатрСва до Вшнiего яковье даял есе еiе огень до огнiцы нашiе Дощ.37 и клишет Матерь Всех к Вышнему, Который дал ей огонь для очагов наших Пiсне хвалы а Матыря спЪваще Тоя красна Птыцiя яква несе ПраЩурем нашем огнь до домы iа... Дощ.7б Песни хвалы и Матерь поет, та прекрасная Птица, которая несла огонь Пращурам нашим в дома их. Матерь Всех, древнерусск. МАТЕР СВА - Матерь Всех (тж. МАТЕР/ МАТРЕ/ МАТР, МАТЫРЕ/ МАТЫРЬ/ МАТЫРЯ, ПТЫЦЯ МАТРЕ СВА; СВА - 1. в роли возвратно-притяжат местоимения свой, ~я, ~ё, ~и, ~их, ~ими и т.п. (ср. санскр. sva свой, собственный; мой, твой, его; n. собственное "я", родственник; собственность 2. все, всё, ~я, притяжат. всех); тж. МАТЫРЕ СВА НЩЕХ - Матерь Всех наших; МАТЫРЬ СЛВА - Матерь Слава; ПТЫЦЯ МАТРЕ СВА - Птица Матерь Всех; МАТЕР СВА СЛАВА - Матерь Всеслава (Всех Слава или Своя Слава). Упоминается только во Влескниге, более сорока раз. "Та прекрасная Птица, которая несла огонь Пращурам нашим в дома их - Тоя красна Птыцiя яква несе ПраЩурем нашем огнь до домы iа", "Матерь Всех поет во Сварге о подвигах ратных". Указывает Русам как поступать. Питар/ Патар, Питар Дий, древнерусск. ПЫТАРЕ ДИИ, тж. ПАТАРЕ/ ПЫТЕРЕ - Небо Отец, Отец Небесный, т.е. Вышень, Сварог. Мн. ч. - питары/ питри (украинск. Петри) - Предки, Пращуры. По-санскритски Дьяус Питар (dyaus небо; pitar отец); в древнерусском определения располагались нормально после определяемого слова, поэтому, вероятно, порядок слов в этом словосочетании изменился на "Питар Дий". Вышень, древнерусск. ВЫШЕНЬ - (ср. санскр. Вишну). Превышний, Единый Бог, Бог Отец, эпитет и аспект Сварога: "НИЕМЯХОМЬ БОЗЯ, РАЗВИЕ ВЫШЕНЬ" - "нет у нас Богов кроме Вышня". См. тж. Сварог. Словарь имен и терминов Влескниги. Н.В. Слатин http://knigavelesa.narod.ru/slatin/slovar_imen_i_terminov.html Ригведа I. 164 46 Индрой, Митрой, Варуной, Агни (его) называют, А оно, божественное, - птица Гарутмант. Что есть одно, вдохновенные называют многими способами. Агни, Ямой, Матаришваной (его) называют. Матаришван (mataricvan) - мифологический персонаж, похитивший в изначальном мире огонь для богов и для Ману Ригведа. Из словаря основных мифологических персонажей и ритуальных понятий. Составила Т.Я. Елизаренкова https://web.archive.org/web/20171122065102/http://www.kirsoft.com.ru/freedom/KSNews_877.htm Матер-Сва-Слава Вся объёмность понятий и представлений наших предков о Земле и Космосе воплощалась в образах почитаемых ими славянских богов. Одного из них – удивительного образа Матери-Сва-Славы – мы намерены коснуться в данном исследовании. Этот образ был до сих пор неизвестен, вернее, настолько забыт, что не упоминался ни в одной из существующих ныне древнеславянских летописей, ни даже в славянском фольклоре и мифологии. Хотя какие-то отголоски его, видимо, сохранились, что позволило исследовательнице Марии Гимбутас в книге «Боги и богини» (изд. в 1973г.) говорить о славянской «великой Птице-Богине», образ которой был раскритикован Б.А. Рыбаковым в силу «недостаточной обоснованности». Но вот «Птица-Богиня» предстаёт перед нами на страницах «Велесовой книги» во всём блеске и красоте! К нашему счастью, не в беглом упоминании вскользь, а в многократных описаниях и повторениях даётся довольно полное представление о сущности, функциях и облике названного божества. МАТЕРЬ-СВА-СЛАВА – Прародительница всех славян. Причём изначально это была совершенно конкретная женщина, матерь Слава, о которой рассказывается в дощ. 9-А: «В давние времена был Богумир, муж Славы, и имел трёх дочерей и двоих сыновей… И мать их, которую звали Славуня, заботилась об их потребностях». Желая выдать дочерей замуж, Богумир отправился на поиски мужей для них. В те времена люди ещё близко общались с богами, и боги принимали непосредственное участие в их судьбе и жизни. И вот Даждьбог послал Богумиру троих небесных вестников – Утренника, Полуденника и Вечерника, за которых вышли замуж дочери Богумира. От них произошли племена древлян, кривичей и полян, а от сыновей – северян и русов. Как уже отмечалось, это были ещё времена матриархата (эпоха его заката), поскольку Богумир назван «мужем Славуни», а не наоборот, и названия племён произошли от имён её дочерей (Древа, Скрева, Полева), а не зятьёв. Датировать этот период можно концом II – началом I тыс. до н.э., поскольку «Велесова книга» сообщает, что роды Богумира и Славуни обитали «за морем в Краю Зелёном» «за две тьмы до Дира» (т.е. за две тысячи лет до Дира, жившего в IX в. н.э.) и «за тысячу триста лет до Германареха» (жил в IV в. н.э.), то есть события происходят в XI–IXв.в. до н.э. Основное занятие обитавших там племён – скотоводство. Поэтому кажущееся на первый взгляд не более чем образным выражение: «мы – потомки Славуни и Даждьбога, родивших нас через корову Земун, и мы были кравенцы (коровичи), скифы (от «скуфе», – «скот» – скотоводы), анты, русы, борусы и сурожцы» (дощ. 7-Є), содержит в себе зашифрованные события прошлого. Славяне действительно произошли от Славуни и в известной мере от Даждьбога, поскольку именно он послал мужей её дочерям, так же, как в своё время послал отрока отцу Тиверцу, имевшего двух незамужних дочерей (дощ. 16). А рождение «через корову Земун» символизирует скотоводческий, пастушеский культ, опять же в его женской ипостаси – Корове, а не Быке – мужском тотеме скотоводов. Эту родословную славяне всегда чтят и помнят: «Мы имеем имя Славы, и славу эту доказали (врагам), идя на железо их и мечи» (дощ. 8/2). «Мы – потомки Славуни, можем быть гордыми и не беречь себя» (дощ. 6-Г). «Мы – потомки рода Славуни, который пришёл к ильмерцам и поселился до (прихода) готов, и был тут тысячу лет» (дощ. 8). (Мы почитаем) «Даждьбога отцом нашим, а матерью – Славу, которые учили нас чтить богов наших, и вели за руку по стезе Прави. Так мы шли и не были нахлебниками, а только славянами, русами, которые богам славу поют и потому суть – славяне» (дощ. 8/2). Таким образом, «Велесова книга» прослеживает самый исток этногенеза славян, раскрывает смысл этого понятия и относит время его возникновения к концу II – началу I тыс. до н.э. С течением веков конкретный первообраз размылся, поэтизировался, возможно, слившись с другими неизвестными нам образами, приобрёл новые черты, поднявшись до уровня божества. Матерь Слава стала МАТЕРЬЮ-СВА-СЛАВОЙ – Всеобщей Матерью, на что указывает определительное местоимение «сва», то есть «вся», «всеохватывающая», «всеобщая», подобно тому, как СВА-РОГ является Всеобщим богом, Творцом всего сущего. В Риг-Веде «висва» также обозначает «весь», например, Висва-Дева – Всебожество. К тому же в Риг-Веде обнаружилась фонетическая аналогия Матери-Сва – МАТАРИШВАН: «Мудрецы дают Единому Сущему многие имена, – это Агни, Яма, Матаришван». Именно функция Дарителя Огня является ключевой как в образе героя древнего индоарийского предания Материшван, похитившего в изначальном мире огонь для богов и первого человека Ману, так и в образе Матери-Сва-Славы, которая на «дощьках» «Велесовой книги» предстаёт в образе Птицы, принесшей на своих крыльях огонь людям. «Матерь – та прекрасная Птица, которая принесла пращурам нашим огонь в дома их, а также агнца /дала», – говорится в дощ. 7-Б. «И вот Магура поёт свою песню к сече, а та Птица послана Индрой. Индра же был и вовек пребудет тем самым Индрой, что передал Перуну все бранные стрелы» (дощ. 6-Г). Здесь Магура – иная ипостась Матери-Сва, её индоарийский вариант. (В иранской мифологии она – Птица Симург). И как Магура является посланницей Индры или Варуны, «летящей в небе на Златом крыле», так и Матерь-Сва является посланницей Вышнего или Патера Дыя-Ондры-Перуна. Здесь обнаруживается общий исток индоарийских образов и прослеживается тенденция их преемственности. «Матерь-Сва обращается к Вышнему…» (дощ. 37-А). «Мы молимся Патеру Дыю, ибо он производит огонь, который Матерь-Сва-Слава принесла на крыльях праотцам нашим» (дощ. 19). Как заботливая мать, она принесла на крыльях небесный огонь для своих детей-славян, которые хранили его в очагах, а также приносили богам в жертву священного агнца, испечённого на огне. Агни у индоарийцев до сих пор бог Огня. Когда славяне ушли из Семиречья в поисках новых земель, Матерь «умных вразумила, храбрых укрепила», а сама полетела впереди, указала благодатные края, освятив новые угодья крылами, и славяне осели там, «как велела Матерь-Сва-Слава» (дощ. 13). По своей сути МАТЕРЬ-СВА-СЛАВА – ЭТО ВОПЛОЩЁННЫЙ В ОБРАЗЕ ПТИЦЫ СИМВОЛ ЧЕСТИ И СЛАВЫ РУСИ. В ней заключена память о подвигах отцов и пращуров, и слава каждого русина, павшего за свою землю, либо прославившего её иными благими деяниями, чудесным образом перетекает к Матери-Славе и становится вечной. «Матерь-Сва сияет ликом, как Солнце, и предвещает нам победы и гибель. Но мы того не боимся, ибо это – земная жизнь, а выше есть жизнь вечная, и потому мы должны радеть о Вечном, ибо земное против него – ничто. Мы на земле, как искры, и сгинем во тьме, будто и не было нас никогда. Только слава наша перетечёт к Матери-Славе и пребудет в ней до конца концов земной и иных жизней» (дощ. 7-Є). Нет ничего прекраснее славы геройства, а русы во все времена проявляли множественные примеры доблести, вот почему Птица сияет оперением, подобно Солнцу, и переливается всеми цветами радуги. «Матерь-Сва распускает крылья, бьёт себя по бокам, и вся сияет нам огненным светом. И каждое перо её иное и прекрасное – КРАСНОЕ, СИНЕЕ, ГОЛУБОЕ, ЖЁЛТОЕ, СЕРЕБРЯНОЕ, ЗОЛОТОЕ И БЕЛОЕ. И сияет, как Солнце-царь, и по колу идёт за Солнцем, и светится семицветьем, завещанным от наших богов» (дощ. 7-Е). Жар-птица из наших сказок – это несомненный отголосок образа Птицы-Славы. Матерь-Сва напоминает русам об их героическом прошлом и зовёт к новым подвигам. В трудный час она приходит на помощь, воодушевляет воинов, предвещает им победу и сама набрасывается на врагов, бьёт их крылами и разит клювом. «Увидели Великую Птицу, летящую к нам, которая набросилась на врагов» (дощ. 14). И русские витязи, прикоснувшись к славе предков, стремясь быть такими же чистыми и сильными душой и телом, идут сражаться за свою землю, за своих жён, детей, отцов, матерей, любимых и, вдохновлённые словами Матери-Сва, вершат ратные подвиги, не жалея ни крови, ни самой жизни. «Как только враг идёт на нас, мы берём мечи и, вдохновлённые словами Матери-Сва, что будущее наше славно, идём на смерть, как на праздник» (дощ. 14). Мы полагаем, что образ Матери-Сва в той или иной мере перешёл во многие более поздние образы славянской мифологии, в частности, полуптиц-полуженщин Вещей Гамаюн, Алконост и Сирин, неземное пение которых заставляет забыть обо всём на свете, причём от голоса Сирин человек может умереть. Дивное пение Матери-Сва действительно воодушевляло воинов, так что смерть на поле боя казалась им праздником, а сила их в сражении увеличивалась десятикратно. В «Велесовой книге» упоминается также образ Берегини (производное от «беречь», «оберегать») – хранительницы памяти о подвигах русов. Она близка к образу Матери-Сва-Славы и связана с ним: «Те славные (воины русские) не берегли ничего, даже жизни своей, – о них говорит Берегиня. – И бьёт крылами Матерь-Сва-Слава и рассказывает потомкам о тех, кто не поддались ни варягам, ни грекам. Говорит та Птица о борусинских героях, которые пали от римлян…» (дощ. 7-Ж). И если Берегиня исполняет конкретную функцию хранительницы памяти о национальных традициях, образе жизни, благих деяниях и ратных подвигах героев во славу Руси, то Матерь-Сва-Слава – более активный образ. Она – побуждение к действию, вместилище энергии, которая проистекает из сохранённой Берегиней славы и памяти. Говоря современным языком, образ Птицы-Сва возникает как определённого рода энергетическое поле, плазменный сгусток, живой, пульсирующий эгрегор в пространстве и времени, «аккумулирующий» волевые и чувственно-образные импульсы отдельных людей в единую субстанцию огромнейшей мощи, сияющую, будто миллионы свечей, будто само Солнце, от которого каждый в свою очередь получает энергетический заряд в качестве «подпитки». В образе Матери-Сва проявляется гармоничное единение личного и общего, славы одного человека и всего народа. Здесь происходит перетекание качественного в количественное и обратно, подобно тому, как все цвета радуги складываются в единый цвет – белый, который, воссияв своей первозданной чистотой и белизной, вновь рассыпается завораживающим семицветьем. Вместе с этим Матерь-Слава представляет собой прямое и непрерывное перетекание Времени из Прошлого – через Настоящее – Будущее, утверждая, что только помня о славе отцов и пращуров и преумножая её сейчас, славяне и впредь останутся такими же славными и сильными. «И бьёт крылами Матерь-Сва-Слава, и рассказывает потомкам о тех, кто не поддались ни варягам, ни грекам. Говорит та Птица о борусинских героях, которые пали от римлян на Дунае у валов трояновых, и полегли без Тризны… Но мы – их сыновья и потомки и также не отдадим землю нашу ни варягам, ни грекам!» (дощ. 7-Ж). Даже в самые тяжёлые времена, когда Русь была окружена со всех сторон врагами, а славяне стали «сирыми и нищими» и не имели сил встать на защиту, Матерь-Сва поддерживала их и звала к подвигам. «Только Птица Матерь-Слава предрекала нам славу и призывала учиться на славе отцов» (дощ. 21). В образе Вещей Птицы она предупреждает о грядущих бедах: «бьёт крылами Матерь-Сва-Слава и предвещает нам тяжкие времена засухи и коровьего мора» (дощ. 28). Также в трудный час она подсказывает важные решения. «Захваченные римлянами и настигнутые готами, мы должны были между двух огней тлеть и сгорать…Тут прилетела к нам Птица Божеская и сказала: “отойдите к полуночи и нападите на них, когда они пойдут на селения наши и пастбища”. Мы так и сделали – отошли к полуночи, а потом напали на них и разбили их» (дощ. 6-А). «Германарех поддержал гуннов, и мы имели двух врагов на обоих концах земли нашей. И Болорев был в великом затруднении: /на кого идти?/. Тут Матерь-Сва прилетела и сказала ему напасть сначала на гуннов, разбить их и повернуть на готов. /И он сделал так/» (дощ. 27). На поле боя русы также часто выстраивали конницу «птицей», – это был вид боевого построения, которому покровительствовала сама Матерь-Сва-Слава. «Мы строимся /по образу/ Матери-Сва, Солнца нашего: простираем “крылья” в обе стороны, а “тело” в середине, а во главе – Ясунь, а по бокам его – воеводы славные…» (дощ. 7-З). «И мы за Сва также шли, выстроив конницу “птицей”, и она врагов “крыльями” накрыла, а “головой” била» (дощ. 20). В тот самый час, когда к воинам, геройски павшим на поле брани, с небес слетает Перуница, неся рог, наполненный «живой водой вечной жизни», Матерь-Сва поёт им величественную Песнь Славы, поёт так, что боги смерти Мор, Мара и Яма отступают перед погибшими, и души их улетают прямо в Сваргу и обретают там вечную жизнь вместе с богами и пращурами. «Матерь-Сва бьёт крылами и славит воинов, которые испили от Перуницы живой воды в сече жестокой» (дощ. 7-Д). После того, как в войнах с готами и гуннами разрушилась великая славянская держава Русколань, просуществовавшая тысячу лет (она была образована во времена Ория в VI в. до н.э. и распалась в IV в. н.э.), русы имели предсказание, что Русколань возродится, «когда Коло Сварожье повернётся к нам, и времена те /за/-Сва придут к нам» (дощ. 36-А). Кто же она – Матерь-Сва-Слава? Грозная воительница или заботливая мать? Прекрасная девица или мудрая жена? Советчица или указчица? И кто она вообще – Женщина, Птица или просто – Сияние? Она – всё! Чаще всего она предстаёт Птицей с женским обликом в блистающем оперении, но вся она многолика и многомерна, она меняется и живёт подобно тому, как существуют, всякий раз меняясь, Огонь, Ветер, Вода, Звёзды, Цветы, Деревья, Звери, Птицы и Люди. Функционально образ Матери-Сва-Славы в чём-то перекликается с образами греческой богини Афины и этрусско-римской Минервы – могучих воительниц, грозных и прекрасных, которые обычно изображались в блестящих шлемах и сверкающих доспехах, со щитом и копьём. Однако они выступают как хранительницы и покровительницы в самом широком смысле. Так и Матерь-Сва-Слава порой изображалась облачённой в защитную броню с крылом в форме щита. Однако она не имеет ни копья, ни меча, ни другого оружия. Сила её воздействия в ином, – в проникновенном слове Пророчества, Восславления и Призыва. С другой стороны, Матерь-Сва-Слава выступает как богиня Победы. «Посмотрите вокруг – и увидите Птицу ту впереди вас, и она поведёт вас к победам над врагами, ибо куда ведёт нас Сва, там одерживаются (победы)» (дощ. 18-А). И в этом она родственна греческой Нике и римской Виктории. Как видим, образ Матери-Сва очень многообразен, и подобная полифункциональность сближает его с Великой Матерью (Ма-Дивой) крито-микенского мира, культ которой сложился, как отмечает академик Б.А. Рыбаков, в середине II тыс. до н.э. Ма-Дивия (или просто Ма) рассматривается, как богиня природы и мать всего живого. Однако в отличие от неё Матерь-Сва выступает не как «богиня всего живого», а как Прародительница только славянского народа, исполняющая функции заботливой матери, хранительницы славы и памяти славянского Рода-Племени. Это именно наша русская Великая Матерь, в образе которой при схожести черт со многими другими божествами присутствуют и черты уникальности. Аналогичного божества нет ни в одной мифологии мира. Есть богини Земли, Плодородия, Охоты, богини-Воительницы и Защитницы, богини-Матери, но ни у кого нет такого объёмного образа богини Славы, от которой произошёл целый народ (в данном случае – славяне). Это указывает на самобытность мировосприятия древних праславян, их уникальную, совершенно самостоятельную философию, которая, органично сосуществуя с прочими религиозно-философскими воззрениями, не растворилась в них, а сохранила особенный, только ей свойственный образ мыслей и взглядов на окружающий мир «Наши боги суть – образы» – говорили предки и устанавливали чаще всего лишь символы своих богов в виде идолов, да и то не всегда. Самой священной иконой для них были Живые Источники, Священные Дубы, Небесные Камни, а храмом – вся Природа. Слишком сложны и многогранны были образы славянских божеств, чтобы запечатлеть их в грубых формах статики хотя бы в одном из многоликих проявлений. Как выразить, к примеру, душу Дерева, запечатлеть мудрость Камня, передать божественное сияние Славы? Вся гамма чувственно-образных понятий передавалась вживую – от поколения к поколению – через волхвов-кудесников, через певцов-сказителей и жила среди славянского народа как неотъемлемая часть их философско-религиозного бытия. Удивительно, но многие из этих образов живут в нас и поныне! В каждом городе и селе есть памятники, обелиски или монументы Славы. Матерь-Слава по-прежнему взирает на нас с высоких курганов в облике Матери-Родины, Женщины-Защитницы, Победительницы, Державницы. Она всегда была, есть и будет Покровительницей Руси. Её дивную песнь и сейчас может услышать каждый, кто чтит своих Богов, Пращуров и своё Отечество. Вот прилетела к нам, Села на древо И поёт Птица, И всякое перо Её – Иное И сияет цветами разными, И стало в ночи, как днём. И поёт она песни, /призывая/ к борьбе и битвам… Услышь, потомок, Песнь Славы И держи в своём сердце Русь, Которая есть И пребудет землёй нашей! (дощ. 8/2) Славянский ведизм и законы Прави / В. Гнатюк, Ю. Гнатюк. Москва : Издательство АСТ, 2020. 288с https://vk.com/doc1271054_549462456 |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5220
Зарегистрирован: 27.08.07
|
|

Отправлено: 30.03.23 15:11. Заголовок: Ригведа, Агни, гимн ..
Ригведа, Агни, гимн апри  Танунапат - зовется отпрыск Асуров; Нарашансой становится он, когда рождается; Матаришваном - когда сформировался в матери; Порывом ветра он стал в (своей) стремительности - III, 29.11 К Агни *** Есть при всем том некоторая часть гимнов РВ, ритуальный характер которых не вызывает сомнений, из них надо прежде всего назвать небольшую группу гимнов-апри (apri букв. умилостивление). Содержание их банально: оно сводится к просьбам к определенным божествам и приглашением их на жертвоприношение. Они неинтересны также в художественном отношении. Смысл их заключается в ином. Формально они примыкают к гимнам Агни, к которому обращены первые три стиха. Апри - название определенного типа литургических гимнов - приглашений ряда божеств на жертвоприношение. Гимны-апри связаны с древним обрядом жертвоприношения животных, который может составлять самостоятельный ритуал или начинать обряд жертвоприношения сомы. В РВ встречается 10 гимнов-апри, причем некоторые стихи и строки переходят из одного гимна в другой. Все эти гимны построены по одной модели. Для каждого стиха задано ключевое слово, набор которых является для данного жанра постоянным. Допустимы лишь очень незначительные варианты ключевого слова в каждом стихе. По этим вариантам, согласно туземной традиции, можно судить о различиях в ритуале у отдельных родов ведийских певцов. Так, в первых трех стихах гимна-апри обращаются к богу огня Агни, который во втором стихе должен быть назван одним из двух священных имен: Нарашанса (naracamsa букв. хвала людей) или Танунапат (tanunapat - сын себя самого). В первом случае в туземном оглавлении гимн называется apram, во втором - apriyah. Лишь изредка могут быть названы оба имени Агни одновременно. По числу ключевых слов гимны-апри могут состоять из 11-ти или 12-ти стихов (Т. Елизаренкова) I, 13 Гимн-апри Группа гимнов I, 12-23 певца Медхатитхи из рода Канвов (Medhatithi Kanva). Размер - гаятри. 1-4 Набор ключевых слов: 1. Прекраснозажженый (susamiddha); 2. Танунапат; 3. Нарашанса; 4. Призванный (ilita) 4 Ману или Манус (manu, manus) - имя родоначальника людей 5…жертвенную солому (barhis) - ключевое слово…Жирноспинную…- Жирноспинная она потому, что ее окропляют жиром 5c Где возникает мир бессмертных! - По ведийским представлениям боги (= мир бессмертных) спускаются на жертвенную солому 6-8 Ключевые слова: 6. Врата (dvaro); 7. Ночь и Ушас (naktosasa); 8. Два хотара (hotara) 8…приглашаю Двух божественных хотаров - По предположению Гельднера, здесь имеются в виду божественный хотар Агни и реальный жрец-хотар 9…богини - ключевое слово. Ида (ila). Nom. pr. Богини, персонифицирующей жертвенное возлияние и молитву. Сарасвати (sarasvati) - Nom. pr. богини молитвы; первоначально персонификация священной реки Ариев РВ. Махи (mahi букв. великая). Имя этой богини встречается наряду с именами Иды и Сарасвати в гимнах апри. Функции ее весьма неотчетливы. Иногда вместо имени Махи в этих гимнах встречается Бхарати 10 Ключевые слова: 10. Тваштар (tvastar); 11. дерево (vanaspati) - подразумевается жертвенный столб; 12. Свага! (svaga) - возглас, приглашающий богов явиться на жертвоприношение 1 Прекраснозажженный привези нам Богов, о Агни, к жертвователю И принеси жертву, о чистый хотар! 2 (Сделай) сладкой, о Танунапат, Нашу жертву у богов, о мудрый! Сделай, чтоб сегодня (ею) насладились! 3 Нарашансу приятного сюда, На эту жертву, я приглашаю, Приготовителя жертвы, с медовым языком. 4 О Агни, на быстроходнейшей колеснице, Призванный, привези богов. Ты - хотар, поставленный Манусом. 5 Расстелите в правильном порядке жертвенную солому, Жирноспинную, о умелые, Где возникает мир бессмертных! 6 Пусть раскроются умножающие космический закон Божественные врата, неиссякающие, - Ныне и впредь - для жертвоприношения! 7 Ночь и Ушас, прекрасно убранных, Я приглашаю на это жертвоприношение, Чтоб они сели на нашу жертвенную солому. 8 Их, Прекрасноязычных, я приглашаю - Двух божественных хотаров, поэтов. Пусть принесут эту жертву для нас! 9 Ида, Сарасвати, Махи - Три богини, приносящие радость, Пусть сядут на жертвенную солому, не ошибающиеся! 10 Тваштара, имеющего все формы, Я приглашаю сюда первым. Пусть будет он только наш! 11 О божественное дерево, Отпусти к богам жертвенное возлияние! Пусть вид дарителя бросится в глаза! 12 (С возгласом) Свага! совершите жертвоприношение Для Индры в доме у жертвователя. Туда я приглашаю богов. I, 142 Гимн-апри Группа гимнов (I, 140-164) Диргхатамаса (dirghatamas - букв. погруженный в глубокий мрак, т.е. слепой), сына Учатхьи (aucathya). Размер - ануштубх 1 Прекраснозажженный, о Агни, привези Сегодня богов (к жертвователю) с поднятым ковшом! Протяни древнюю нить Для почитателя, выжавшего сому! 2 О Танунапат, отмерь Жирную, сладкую Жертву у вдохновенного, вроде меня, Старающегося (при обряде) почитателя! 3 Чистый, светлый, удивительный Нарашанса смешивает жертву С медом трижды в день, Бог, достойный жертв среди богов. 4 Призванный, о Агни, привези Сюда Индру, яркого, любимого! Ведь эта моя молитва к тебе Пробирается, о прекрасноязыкий! 5 С поднятым ковшом расстилая Жертвенную солому при жертвоприношении во время прекрасного обряда, Я переворачиваю (ее, чтоб она дала) больше места богам, (Чтобы стала) широкой защитой для Индры. 6 Пусть раскроются умножающие (вселенский) закон, - Чтобы боги могли пройти - великие Чистые, многожеланные Врата, божественные, неиссякающие! 7 Радостно прославляемые, близкие (друг другу) Ночь и Ушас, прекрасно убранные, Самые юные (дочери) закона, матери (его) Пусть усядутся вместе на жертвенную солому! 8 Два сладкоязычных прославляющих Божественных хотара-поэта. Пусть принесут эту жертву для нас Сегодня достигающую цели, касающуюся неба! 9 Чистая, помещенная среди богов Хотра, среди Марутов - Бхарати, Ида, Сарасвати, Махи (- богини) Пусть сядут на жертвенную солому, достойные жертв! 10 Это наше удивительное семя, Многожды многое само по себе, Тваштар пусть развяжет для процветания, Для блага, у нас на пупе, (он,) преданный нам! 11 Само отпуская (жертвенное животное), Почти богов, о дерево! Пусть Агни сделает вкусными жертвенные возлияния, Бог, мудрый среди богов! 12 Для сопровождаемого Пушаном, Марутами, Всеми-Богами, Ваю, Для трепещущего от напева гаятри Индры Совершите жертвенное возлияние (с возгласом) Свага! 13 Приди, чтобы отведать, Жертвенные возлияния, приготовленные (под возглас) Свага! О Индра, приди, услышь зов! Тебя зовут во время обряда. I, 188 Гимн-апри Группа гимнов I, 165-191 Агастьи. Агастья (agastya) говорит о себе как об отпрыске рода Маны (manya) или сыне Маны (mana). Он выступает как действующее лицо в нескольких гимнах этой группы. Размер - гаятри 1 Зажженный, ты царствуешь сегодня Как бог вместе с богами, о завоевывающий тысячу. Как вестник, поэт, отвези жертвы! 2 О Танунапат, для идущего (путем) закона Медом обмазывается жертва. Дающая тысячные услады. 3 Политый (маслом), достойный наших призывов, Привези богов, достойных жертв! О Агни, ты - захватчик тысяч! 4 С силой они разостлали обращенную к востоку Жертвенную солому, достаточную для тысячи мужей, Где вы, о Адитьи, царите. 5 Царящие отдельно, царящие вместе, просторные, могучие, Многие и (те,) кого еще больше. - Врата истекали струями жира. 6 С прекрасными золотыми ожерельями, прекрасно убранные (Эти) две царствуют благодаря (своей) красоте. Пусть Ушас и (Ночь) усядутся здесь! 7 Ведь (это) два первых сладкоречивых Хотара, два божественных поэта - Пусть пожертвуют они эту нашу жертву! 8 О Бхарати, Ида, Сарасвати, Вы все (те богини,) к кому я обращаюсь, Поощрите нас к красоте! 9 Ведь Тваштар - могучий (творец) видов - Он создал всех животных. Пожертвуй нам их процветание! 10 Само по себе, о дерево, Отпусти (жертвенное животное) под защиту к богам! Пусть Агни сделает жертвы вкусными! 11 Агни, идущий впереди богов, Умащается пением гаятри. Он сверкает под возгласы: Свага! II, 3 Гимн-апри Размер - триштубх, стих 7 - джагати 2d Да умастит он всех богов - sаm anaktu devаn - Букв, да соединит он богов, умащая (их) 3d Принесите жертву...о мужи! - Обращение к жрецам 4b...несущая прекрасное бремя - subhаram - т.е. несущая на себе богов 5b врата - dvаro 5d Очищая славную варну - varna - букв. цвет - обозначение социальной группы людей (первоначально по цвету их кожи) 6c-d Ткут они...нить. Украшение жертвы... - Как поясняет Гельднер, натянутая нить - это время, а пестрый узор, который ткут на основе, украшение - это само жертвоприношение 7d На пупе земли nabha prthivyah - На месте жертвоприношения…На трех вершинах! - На трех жертвенных кострах 9b Во исполнение...(молитв) рождается сын - Сын vira - основное значение этого слова муж, мужчина, герой 10a…дерево vanaspati - Подразумевается жертвенный столб, к которому привязано жертвенное животное 11 - Свага! - svаha - возглас, приглашающий богов явиться на жертвоприношение 1 Зажженный, помещенный на землю, Агни Стоит, обращенный ко всем существам. Чистый хотар, (существующий) от века, очень мудрый Бог Агни пусть принесет жертву богам, (он,) достойный! 2 Нарашанса, смазывающий (все) места (жертвы), (Своим) величием уравновешивает три неба, (он,) прекрасно-пламенный, Орошающий жертву мыслью, кропящею жиром, - Да умастит он всех богов во главе жертвы! 3 Призванный, о Агни, нашей мыслью как достойный, Принеси сегодня жертву богам, (находясь) впереди человеческого (хотара)! Привези несотрясаемую толпу Марутов! Принесите жертву Индре, восседающему на соломе, о мужи! 4 О божественная жертвенная солома, возрастающая, дающая богатство из мужей, Разостланная для богатства на этом алтаре, несущая прекрасное бремя, - О Васу, сядьте на нее, умащенную жиром, О Все-Боги, Адитьи, достойные жертв! 5 Широко растворитесь, призываемые Божественные врата, дарующие приятный вход благодаря (нашим) поклонам! Да расступятся, (чтобы быть) просторными, нестареющие (врата), Очищая славную варну, богатую прекрасными мужами! 6 Ушас и Ночь, возросшие от века, (творят) для нас (Свои) благие деяния: словно две радостные ткачихи Ткут они вместе натянутую нить, Украшение жертвы, (они,) две дойные коровы, полные молока. 7 Два первых божественных хотара, более сведущих, Пусть правильно принесут жертву вместе с гимном, (они,) более прекрасные! Принося жертвы богам в урочное время, пусть они вместе умастят (жертву) На пупе земли, на трех вершинах! 8 Сарасвати, приводящая к успеху нашу поэтическую мысль, Богиня Ида, Бхарати, все преодолевающая, - Три богини, усевшись по своему желанию на эту жертвенную солому, Пусть охраняют нас надежною защитой! 9 Коричневатый, которого легко носить, наделяющий жизненной силой, - Во исполнение (наших молитв) рождается сын, любящий богов. Да развяжет у нас Тваштар пуповину - потомство! Да отправится также (жертвенное животное) на попечение богов! 10 Пусть присутствует дерево, (легко) отпускающее (жертвенное животное)! Пусть Агни под воздействием поэтических мыслей сделает жертву вкусной! Пусть божественный разделыватель туши, зная путь, Приведет к богам жертву, трижды умащенную! 11 Жир присущ (Агни), жир - его лоно, В жире он пребывает, жир - его место. По своему желанию привези богов! Опьяняйся! О бык, увези жертву, над которой возгласили: Свага! III, 4 Гимн-апри Гимны этой мандалы по традиции приписывается Вишмамитре, сыну Гатхина (Vicvamitra Gathina), внуку Кушики (Kucika). Размер - триштубх. О жанре гимнов-апри см. примеч. I, 13. Данный гимн принадлежит к разновидности априя 8a Бхарати вместе с женами, происходящими от Бхараты (a bharati bharatibhih) - Бхарати в ед. ч. - nom. pr. богини речи и хвалебной песни, ключевое слово этого стиха. Во мн. ч. это имя встречается в РВ только здесь (повторено в VII, 2). По Саяне, это жены, происходящие от Бхараты (bharata - nom. pr. Родоначальника), т.е. Сурьи, притом что Бхаратой или происходящим от Бхараты (bharata) нередко называют Агни. Ср. аналогичную синтаксическую структуру в 8c 1 С каждым поленом становись расположенным к нам! С каждой вспышкой пламени передавай (нам) благосклонность Васу! О бог, богов привези для жертвоприношения! Как друг друзей почитай, будучи благосклонным, о Агни! 2 (Ты,) кого боги трижды в день используют, жертвуя День за днем, - Варуна, Митра, Агни - Сделай эту нашу жертву полной сладости, О Танунапат, имеющей лоно из жира, служащей (богам)! 3 Продвигается вперед молитва, для всех желанная, Чтобы первым почтить хотара Иды, Чтобы с поклонениями приветствовать быка. Пусть принесет он жертву богам, призванный как лучший жертвователь! 4 Пусть для вас двоих во время обряда сделан он направленным вверх. Языки пламени, продвигающиеся через пространства, вверх. Или же на пупе земли уселся хотар. Мы раскладываем жертвенную солому, образующую место для богов. 5 Мыслью выбирая семь обязанностей хотара, Все вдохновляя, пусть вернутся (боги) в соответствии с законом! Пусть направятся они на эту жертву через многие (врата), Украшенные мужами, возникшие на жертвенных раздачах! 6 Восхваляемые Ушас (и Ночь), тесно связанные, (друг с другом,) при(ходят) И улыбаются (нам обе,) несхожие телом, Чтобы Митра, Варуна у нас радовались, А также Индра с Марутами - их величию. 7 Двух первых божественных хотаров я подчиняю себе. Семеро наделенных жизненной силой опьяняются по своему усмотрению. Прославляя закон, закон они и возглашают, Как хранители завета, следя мыслью за заветом. 8 Пусть Бхарати вместе с женами, происходящими от Бхараты, Ида вместе с богами, Агни вместе с людьми, Сарасвати с потомками Сарасвата, Три богини усядутся здесь на эту жертвенную солому! 9 А ты, бог Тваштар, щедро развяжи нам Это плодородное семя, Из которого рождается сын, способный к работе, Наделенный прекрасной силой действия, запрягающий давильный камень, любящий богов! 10 О дерево, отпусти к богам (жертвенное животное)! VII, 2 Гимн-апри Гимны этой мандалы по традиции приписываются Васиштхе (Vasistha букв. лучший и его потомкам. Большинство гимнов Мандалы VII по анукрамани приписываются самому Васисштхе. Размер - триштубх …8-11 = III, 4, 8-11 1 Наслаждайся сегодня нашим поленом, о Агни! Гори высоко, вздымая дым, достойный (почитания)! Касайся небесной вершины (своими) вихрами, Притяни (их) вместе с лучами солнца! 2 Величие среди этих (богов) Нарашансы, достойного почитания, Мы будем прославлять с помощью жертв, (Среди) богов, которые, обладая прекрасной силой духа, чистые, дающие вдохновение, Делают вкусными приношения обоего рода. 3 Асуру, достойного призывов у вас, прекрасного силой действия, Возглашающего правду вестника, (движущегося) между двух миров, Агни, зажженного (некогда) Ману, подобно Ману, Мы хотим всегда возвеличить для обряда. 4 Оказывая уважение, принося (дары), коленопреклоненно, Они раскладывают с поклонением жертвенную солому вокруг огня. Поливая жирноспинную (жертвенную солому), крапчатую (от жира), Адхварью, натирайте (ее) возлиянием! 5 Доброжелательные, преданные богам они растворили Врата, жаждя (божественной) колеснице для богослужения. Словно две матери, облизывающие теленка, Словно девицы (украшающиеся) на празднествах, они умащают многие (врата). 6 И две юные божественные жены, две великие (богини) Ушас и Ночь, подобные хорошо доящейся корове, Сидящие на жертвенной соломе, многопризываемые, щедрые, Достойные жертв, - пусть они приникнут к нам для (нашей) удачи! 7 Два вдохновенных (хотара), два поэта на жертвоприношениях у людей, - Я думаю о вас, о двух Джатаведасах, чтоб почтить. Сделайте наш обряд устремленным вверх при призывах (богов)! Вы двое добываете у богов желанные блага. 8 Пусть Бхарати вместе с женами, происходящими от Бхараты, Ида вместе с богами, Агни вместе с людьми, Сарасвати с потомками Сарасвата, Три богини усядутся здесь на эту жертвенную солому! 9 А ты, бог Тваштар, щедро развяжи нам Это плодородное семя, Из которого рождается сын, способный к работе, Наделенный прекрасной силой действия, запрягающий давильный камень, любящий богов! 10 О дерево, отпусти к богам (жертвенное животное)! Пусть Агни-заклатель сделает жертву вкусной! И пусть он также - хотар более истинный, (чем хотар-человек,) - принесет жертву, Ведь он знает поколения богов. 11 Зажженный, о Агни, приезжай к нам сюда Вместе с Индрой, с могучими богами на одной колеснице! Да усядется на нашей жертвенной соломе Адити, благословенная сыновьями! (С возгласом:) Свага! пусть опьяняются бессмертные боги! IX, 5. Гимн-апри Автор по анукрамани, Асита, потомок Кашьяпы (Asita Kacyapa) или Девала, потомок Кашьяпы (Devala Kacyara). Особенность этого гимна в том, что при формальном соблюдении схемы ключевых слов гимнов-апри он остается гимном соме. Имя Павамана (pavamana букв. очичающийся (от pu, pavate, punati)) встречается в каждом его стихе. Размер: стихи 1-7 гаятри, 8-11 ануштубх 1 Зажженыи, господин со всех сторон, Павамана ярко сверкает, Радуя (всех), (этот) громко ревущий бык. 2 Танунапат-Павамана Течет, оттачивая рога, По воздуху, красуясь. 3 Достойный призывов Павамана, Блистательное богатство, ярко сверкает, Со (своими) потоками сладости - мощно, 4 Мощно расстилая обращенную к востоку Жертвенную солому, золотистый Павамана, Бог движется среди богов. 5 Высоко раскрываются (своими) створками Золотые божественные врата, Прекрасно восхваленные Паваманой. 6 Павамана страстно желает Двух нарядных, высоких, великих - Ночь-и-Ушас, словно двух прекрасных (женщин). 7 Обоих богов со взглядом героя, Двоих божественных хотаров зову я. Павамана - (это) Индра бык. 8 Бхарати, Сарасвати, Ида великая пусть придут На это наше жертвоприношение Паваманы, Три богини, прекрасно украшенные. 9 Тваштара, перворожденного пастыря, Шествующего впереди, я призываю. Капля - (это) Индра, бык золотистый. Павамана - (это) Праджапати. 10 Дерево, о Павамана, Обмажь кругом сладким потоком, (Дерево) с тысячей ветвей, зеленое, Сверкающее, золотое! 11 О Все-Боги, приходите На провозглашение: Свага! у Паваманы: Ваю, Брихаспати, Сурья, Агни, Индра единодушные! X, 70 Гимн-апри Группа гимнов (X, 69-70) Сумитры, сына Вадхрьяшвы (Sumitra Vadhryacva). Размер - триштубх 1 Наслаждайся сегодня моими дровами, о Агни! На месте жертвенного питья с радостью прими обмазанную жиром (жертвенную ложку)! Ввысь устремись на вершине земли в счастливейший из дней, О (бог) с прекрасной силой духа, для почитания богов! 2 Как едущий впереди богов пусть приедет сюда Нарашанса на конях разного цвета! Пусть на пути закона лучший из богов Сделает жертвенное блюдо вкусным для богов благодаря поклонению! 3 Люди, имеющие жертву, постоянно Призывают Агни к службе вестника. На конях, возящих лучше всех, на прекрасно катящейся колеснице, Привози богов (и) усаживайся здесь хотаром! 4 Пусть распространится поперек радующая богов (жертвенная солома)! Длинная в длину, пусть она будет благоухающей для нас! С нераздраженным духом, о божественная жертвенная солома, Почти жаждущих богов с Индрой во главе. 5 Коснись поверхности неба (и) еще дальше, Или же раскройтесь, насколько простирается земля! О врата, желающие (этого), задержите (своим) могуществом. Вместе с могучими (богами) божественную колесницу, стремясь к (этой) колеснице! 6 Пусть две божественные дочери неба, хорошо украшенные Ушас и Ночь, усядутся на излюбленном месте (Агни)! Пусть жаждующие боги, о вы, две жаждующие, Усядутся на вашем широком лоне, о вы, приносящие счастье. 7 Высоко вверх (поднят) давильный камень, зажжен огонь. Приятны установления в лоне Адити. О два жреца, поставленные впереди на этом жертвоприношении, Знающие больше других, добудьте богатство с помощью жертв. 8 О три богини, на эту жертвенную солому Сядьте пошире! Мы сделаем вам (ее) мягкой. Пусть радуются они - (среди них) Ида - богиня со следами, пропитанных жиром, - Жертве, как у Мануса, (и) хорошо предложенным возлиянием! 9 О бог Тваштар, поскольку ты достиг привлекательности (формы), Поскольку ты стал сотоварищем Ангирасов, При(веди) (это жертвенное животное) в область богов как знаток! Охотно приноси жертвы, о даритель богатства, (ты,) у кого прекрасные сокровища! 10 О лесное дерево, привязав (жертвенное животное) веревкой, Приведи (его) в область богов как знаток! Пусть бог сделает вкусными, пусть приготовит возлияния! Пусть Небо-и-Земля помогут моему призыву! 11 О Агни, приведи Варуну для нашего усиления, Индру с неба, Марутов из воздушного пространства! Пусть усядутся на жертвенную солому все достойные жертв! Свага! - пусть опьяняются бессмертные боги! X, 110 Гимн-апри Автор, по анукрамани - Джамадагни из рода Бхригу (Jamadagni Bhargava) или Рама, сын Джамамадагни (Rama Jamadagnya). Размер - триштубх 1 Прекраснозажженный сегодня в доме человека, Бог, ты почитаешь богов, о Джаведас. Привози богов, понимая (в этом), о великий как Митра! Ты вестник, поэт прозорливый. 2 О Танунапат, умащая медом исхоженные Пути закона, сделай (жертву) вкусной, о прекрасноязыкий! Принося успех молитвам и жертве благодаря поэтическим видениям, Направь наш обряд к богам! 3 Поливаемый жиром, достойный призывов и прославлений, Приди, о Агни, единодушный с Васу! Ты хотар богов, о юный. Приноси им жертвы, побужденный (к этому) как жертвующий лучше! 4 На восток в направлении земли перекладывается Жертвенная солома в это самое утро в начале дней. Она распространяется все дальше, все шире, Как мягкое (ложе) для богов, для Адити. 5 Пусть просторные широко раскроются, Как украшающие себя жены для мужей! О божественные врата, высокие, всему благоприятствующие. Дайте богам удачно пройти! 6 Пусть плодородные, достойные жертв, тесно связанные (друг с другом) Ушас-и-Ночь усядутся на свое лоно! Две божественные юные жены, высокие, с чудесными золотистыми украшениями, Облачающиеся в красоту сверкающих драгоценностей! 7 Два божественных хотара, первые, красноречивые, Отмеряющие жертву человека, чтобы приносить жертвы, Два певца, вдохновляющие на жертвенных раздачах, Указующие (своим) указанием свет, обращенный на восток… 8 Пусть быстро придет на наше жертвоприношение Бхарати, (А также) Ида, проявляющая себя здесь, как при Манусе! Три богини, - (среди них) Сарасвати - пусть усядутся здесь На этой удобной жертвенной соломе, (они,) искусные! 9 Кто этих двоих родителей - Небо-и-Землю - Украсил формами, (а также) все существа, Того сегодня, о хотар, посланный как лучше жертвующий, (Этого) бога Тваштара почти здесь как знаток! 10 Отпусти по своему почину (жертвенное животное) Под покровительством богов, умащая жертвоприношения в положенное время! Лесное дерево, заклатель, бог Агни, - Пусть сделают они жертву вкусной благодаря меду (и) жиру! 11 Едва успев родиться, он отмерил жертву. Агни стал идущим впереди богов. По указанию этого хотара, по слову вселенского закона Пусть боги вкушают возлияние, сопровождаемое возгласом: Свага! РигВеда. Инвариантность. Гимн-апри https://web.archive.org/web/20170709051347/http://kirsoft.com.ru/freedom/KSNews_881.htm |  |

|
|
Ять
|

| постоянный участник


|
Пост N: 5222
Зарегистрирован: 27.08.07
|
|

Отправлено: 02.04.23 07:00. Заголовок: Первый гимн Ригведы ..
Первый гимн Ригведы  Ригведа I, 1. К Агни Тема — Агни. Размер — гаятри Ригведа начинается гимном Агни, который восхваляется здесь как бог жертвенного огня, руководитель жертвоприношения, божественный жрец, охватывающий жертву своим пламенем и дымом передающий ее богам. Агни приглашает богов на жертвоприношение и дает награду (дакшину) за него. Первые пять стихов гимна начинаются с имени Агни в разных падежах, в стихе 6 даются звуковые намеки на него: anga angirah, в стихах 7, 9 его имя представлено звательной формой. И содержание, и форма гимна преследуют одну цель — призвать Агни на жертвоприношение 1 Агни, призываю…бога…жреца…Хотара (agnim ile purahitam / yajnasya devam rivijam / hotaram rainadhatamam. Хотар — технический термин для обозначения главного жреца царя (от hu- «совершать жертвенное возлияние»)…призываю (ile)… — и одновременно: «молю», «восхваляю» 2…риши (r’si)… — букв, «мудрец», «провидец», «певец» (гимнов); к авторитету прежних риши не раз апеллировали слагатели гимнов РВ; в разных родах риши, передаваясь из поколения в поколение, тысячелетия хранилась РВ 3…он… — sc. жертвователь 4…обряд (adhvara-)… — Здесь имеется в виду совокупность ритуальных действий, осуществляемых жрецами-адхварью, или же торжественное шествие при жертвоприношении (ср. adhvan- «путь») 5с Бог с богами да придет! — Часто повторяющийся в РВ рефрен 6 Ангирас — т.е. принадлежащий к классу полубогов, славившихся замечательным пением, постоянный эпитет Агни в РВ; в ед. ч., возможно, также nom. pr. знаменитого жреца 8 К царящему (rajantam от raj- «царить»)… — Или «к сверкающему» (от raj- «сверкать»). Как отмечает Рену, значения этих двух корней налагаются друг на друга, когда речь идет о божествах света 9 Как отец — сыну… — Нередко тот, кто приносит жертву Агни, считался его сыном (а иногда, наоборот, его отцом), а дом, где зажигался огонь, считался для Агни «своим домом» — ср. 8с 1 Агни призываю я - во главе поставленного Бога жертвы (и) жреца, Хотара обильнейшесокровищного. 2 Агни достоин призываний риши - Как прежних, так и нынешних: Да привезет он сюда богов! 3 Агни, посредством (него) пусть достигает он богатства И процветания - изо дня в день - Сияющего, мужеобильнейшего! 4 О Агни, жертва (и) обряд, Которые ты охватываешь со всех сторон, Именно они идут к богам. 5 Агни-хотар с прозорливостью поэта, Истинный, с ярчайшей славой, - Бог с богами да приидет! 6 Когда ты в самом деле возжелаешь, О Агни, сделать добро почитающему (тебя), То у тебя это истинно, о Ангирас. 7 К тебе, о Агни, изо дня в день, О озаряющий тьму, мы приходим С молитвой, неся поклонение - 8 К царящему при обрядах, К пастырю закона, сверкающему, К возрастающему в доме своем. 9 Как отец - сыну, О Агни, будь доступен нам! Сопровождай нас ради блага! |  |

|
|
Ответов - 300
, стр:
1
2
3
4
5
6
7
8
9
10
All
[только новые]
|
|
|



